
【题目】如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
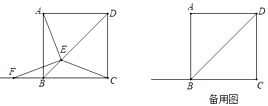
(1)求证:CE=EF;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求△BEF面积的最大值.
【答案】(1)见解析;(2)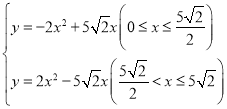 ;(3)50
;(3)50
【解析】
(1)作辅助线,构建三角形全等,证明△AEM≌△EFN和△ADE≌△CDE(SAS),可得AE=CE=EF;
(2)分两种情况:根据三角形的面积公式可得y与x之间关系的函数表达式,根据勾股定理计算BD的长可得x的取值;
(3)根据(2)中的两种情况,分别利用配方法和二次函数的增减性可得结论.
(1)证明:过E作MN∥AB,交AD于M,交BC于N,
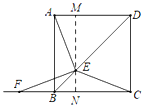
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:BD=![]() ,
,
∴0≤x≤5![]() ,
,
由题意得:BE=2x,
∴BN=EN=![]() x,
x,
由(1)知:△AEM≌△EFN,
则AE=EF=EC,
分两种情况:
当0≤x≤ ![]() 时,如图1,
时,如图1,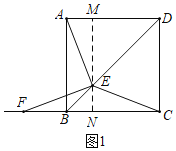
∵AB=MN=10,
∴ME=FN=10﹣![]() x,
x,
∴BF=FN﹣BN=10﹣![]() x﹣
x﹣![]() x=10﹣2
x=10﹣2![]() x,
x,
∴y=![]() =﹣2x2+5
=﹣2x2+5![]() x(0≤x≤
x(0≤x≤![]() );
);
当![]() 时,如图2,过E作EN⊥BC于N,
时,如图2,过E作EN⊥BC于N,
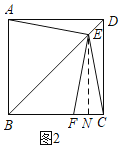
∴EN=BN=![]() x,
x,
∴FN=CN=10-![]() x,
x,
∴BF=BC-2CN=10-2(10-![]() x)=
x)=![]() x-10,
x-10,
∴y=![]() =2x2-5
=2x2-5![]() x(
x(![]() );
);
综上,y与x之间关系的函数表达式为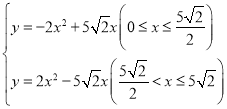
(3)①当0≤x≤ ![]() 时,如图1,
时,如图1,
∴y=﹣2x2+5![]() x=﹣2(x﹣
x=﹣2(x﹣![]() )2+
)2+![]() ,
,
∵﹣2<0,
∴当x=![]() 时,y有最大值是
时,y有最大值是![]() ;
;
当![]() 时,如图2,
时,如图2,
∴y=﹣2x2+5![]() x=2(x﹣
x=2(x﹣![]() )2-
)2-![]() ,
,
∵2>0,
∴当x=![]() 时,y有最大值是50;
时,y有最大值是50;
即△BEF面积的最大值是50.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
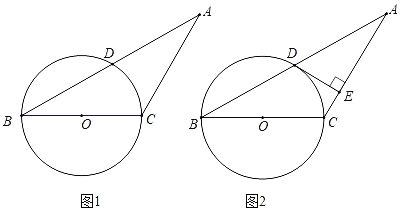
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年新冠肺炎疫情发生以后,各级财政部门按照党中央国务院的决策部署,迅速反 应、及时应对.2月14日下午,国务院联防联控机制就加大疫情防控财税金融支持 力度召开新闻发布会.会上,财政部应对疫情工作领导小组办公室主任、社会保障 司司长符金陵透露,财政部建立了全国财政系统疫情防控经费的日报制度,实时跟踪各地方经费保障情况,截至2月13日各级财政共计支出了805.5亿元保障资金,其中805.5亿元用科学记数法表示正确的是( )
A.![]() 元B.
元B.![]() 元
元
C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 出发沿
出发沿![]() 方向在运动速度为3个单位/秒,点
方向在运动速度为3个单位/秒,点![]() 从
从![]() 出发向点
出发向点![]() 运动,速度为1个单位/秒,
运动,速度为1个单位/秒,![]() 、
、![]() 同时出发,点
同时出发,点![]() 到点
到点![]() 时两点同时停止运动.
时两点同时停止运动.
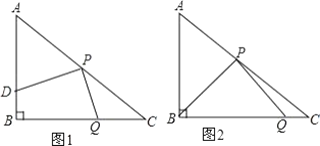
(1)点![]() 在线段
在线段![]() 上运动,过
上运动,过![]() 作
作![]() 交边
交边![]() 于
于![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(2)运动![]() 秒后,
秒后,![]() ,求此时
,求此时![]() 的值;
的值;
(3)![]() ________时,
________时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
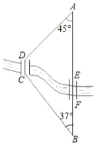
【题目】如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
(1)求点D到直线AB的距离;
(2)现在从A地到B地可比原来少走多少路程?
(结果保留小数点后一位.参考数据:![]() ≈1.41,sin37°≈0.60,cos37°≈0.80).
≈1.41,sin37°≈0.60,cos37°≈0.80).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com