
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.
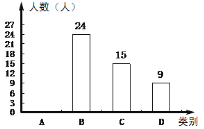
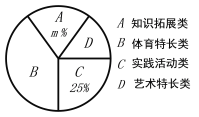
(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
科目:初中数学 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用![]() 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用![]() 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价![]() 元,最后剩下
元,最后剩下![]() 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
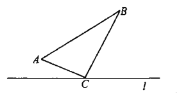
【题目】如图,![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 路径向终点
路径向终点![]() 运动;点
运动;点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动.点
运动.点![]() 和
和![]() 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .则点
.则点![]() 运动时间等于____________时,
运动时间等于____________时,![]() 与
与![]() 全等。
全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.
(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线。
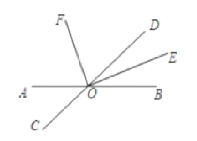
(1)∠DOE的补角是___;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
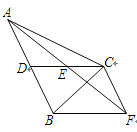
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度![]() (cm)与所挂物体的质量
(cm)与所挂物体的质量![]() (kg)之间的关系如下表:
(kg)之间的关系如下表:
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
弹簧的长度 | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com