
| 运行区间 | 公布票价 | 学生票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 三等座 |
| 无锡 | 上海 | 81(元) | 68(元) | 51(元) |
分析 (1)设参加社会实践的老师有m人,学生有n人,则学生家长有2m人,若都买二等座单程火车票且花钱最少,则全体学生都需买二等座学生票,根据题意得到方程组:$\left\{\begin{array}{l}{81(3m+n)=17010}\\{68×3m+51n=11220}\end{array}\right.$,求出方程组的解即可;
(2)有两种情况:①当180≤x<210时,学生都买学生票共180张,(x-180)名成年人买二等座火车票,(210-x)名成年人买一等座火车票,得到解析式:y=51×180+68(x-180)+81(210-x),②当0<x<180时,一部分学生买学生票共x张,其余的学生与家长老师一起购买一等座火车票共(210-x)张,得到解析式是y=-30x+17010;
(3)由(2)小题知,当180≤x<210时,y=-13x+13950和当0<x<180时,y=-30x+17010,分别讨论即可.
解答 解:(1)设参加社会实践的老师有m人,学生有n人,则学生家长有2m人,若都买二等座单程火车票且花钱最少,则全体学生都需买三等座学生票,依题意得:$\left\{\begin{array}{l}{81(3m+n)=17010}\\{68×3m+51n=11220}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=10}\\{n=180}\end{array}\right.$,
则2m=20,
答:参加社会实践的老师、家长与学生分别有10人、20人、180人.
(2)解:由(1)知所有参与人员总共有210人,其中学生有180人,
①当180≤x<210时,最经济的购票方案为:
学生都买学生票共180张,(x-180)名成年人买二等座火车票,(210-x)名成年人买一等座火车票.
∴火车票的总费用(单程)y与x之间的函数关系式为:y=51×180+68(x-180)+81(210-x),
即y=-13x+13950(180≤x<210),
②当0<x<180时,最经济的购票方案为:
一部分学生买学生票共x张,其余的学生与家长老师一起购买一等座火车票共(210-x)张,
∴火车票的总费用(单程)y与x之间的函数关系式为:y=51x+81(210-x),
即y=-30x+17010(0<x<180),
答:购买火车票的总费用(单程)y与x之间的函数关系式是y=-13x+13950(180≤x<210)或y=-30x+17010(0<x<180).
(3)由(2)小题知,当180≤x<210时,y=-13x+13950,
∵-13<0,y随x的增大而减小,
∴当x=209时,y的值最小,最小值为11233元,
当x=180时,y的值最大,最大值为11610元.
当0<x<180时,y=-30x+17010,
∵-30<0,y随x的增大而减小,
∴当x=179时,y的值最小,最小值为11640元,
当x=1时,y的值最大,最大值为16980元.
所以可以判断按(2)小题中的购票方案,购买一个单程火车票至少要花11233元,最多要花16980元,
答:按(2)小题中的购票方案,购买一个单程火车票至少要花11233元,最多要花16980元.
点评 本题主要考查对一次函数,二元一次方程组,一元一次不等式等知识,解题的关键是理解题意,学会构建方程组或一次函数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
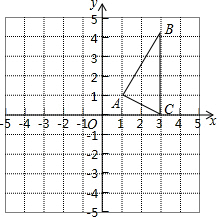 在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).
在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
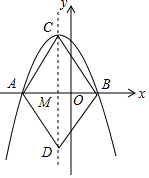 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-2,0),B(1,0),顶点为C,对称轴于x轴交于点M,连接AC,BC,作AD∥BC交对称轴于点D,连接BD,有下列5个结论:①a-b=0;②当-2<x<1时,y>0;③四边形ADBC是菱形;④9a-3b+c>0;⑤c=2a,其中正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-2,0),B(1,0),顶点为C,对称轴于x轴交于点M,连接AC,BC,作AD∥BC交对称轴于点D,连接BD,有下列5个结论:①a-b=0;②当-2<x<1时,y>0;③四边形ADBC是菱形;④9a-3b+c>0;⑤c=2a,其中正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
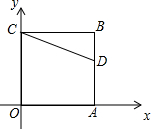 如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然事件 | B. | 不可能发生 | C. | 可能发生 | D. | 很可能发生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com