
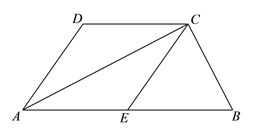
【题目】如图,在四边形ABCD中,AD⊥CD,BC⊥CD,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F。
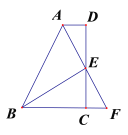
证明:(1)FC=AD;
(2)AB=BC+AD。
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
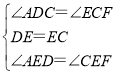 ,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】已知直线 l1 经过点 A(5,0)和点 B(![]() ,﹣5)
,﹣5)
(1)求直线 l1 的表达式;
(2)设直线 l2 的解析式为 y=﹣2x+2,且 l2 与 x 轴交于点 D,直线 l1 交 l2 于点 C, 求△CAD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备了50个签,其中甲类、乙类、丙类按名额设置、25个空签,采取抽签的方式来确定名额分配,请解决下列问题
(1)该班小明同学恰好抽到丙类名额的概率是多少?
(2)该班小丽同学能有幸去参加游学活动的概率是多少?
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到20%,则还要争取甲类名额多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
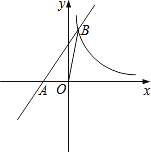
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 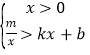 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是![]() ,则点C的坐标是( )
,则点C的坐标是( )

A. (4,2) B. (2,4) C. (![]() ,3) D. (3,
,3) D. (3,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com