
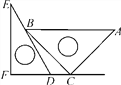
【题目】一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12![]() ,试求CD的长.
,试求CD的长.
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC边的中点,点E,F分别在AD及其延长线上,且CE∥BF,连接BE,CF.
(1)求证:四边形EBFC是菱形;
(2)若BD=4,BE=5,求四边形EBFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在射线OM、ON上运动(不与点O重合).
(1)如图1,若∠MON=90°,∠OBA、∠OAB的平分线交于点C,则∠ACB= °;
(2)如图2,若∠MON=n°,∠OBA、∠OAB的平分线交于点C,求∠ACB的度数;
(3)如图2,若∠MON=n°,△AOB的外角∠ABN、∠BAM的平分线交于点D,求∠ACB与∠ADB之间的数量关系,并求出∠ADB的度数;
(4)如图3,若∠MON=80°,BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E.试问:随着点A、B的运动,∠E的大小会变吗?如果不会,求∠E的度数;如果会,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,有下列说法:①点
,有下列说法:①点![]() 与点
与点![]() 的距离是线段
的距离是线段![]() 的长;②点
的长;②点![]() 到直线
到直线![]() 的距离是线段
的距离是线段![]() 的长;③线段
的长;③线段![]() 是
是![]() 边
边![]() 上的高;④线段
上的高;④线段![]() 是
是![]() 边
边![]() 上的高.
上的高.
上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( )

A. DA=DEB. BD=CEC. ∠EAC=90°D. ∠ABC=2∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
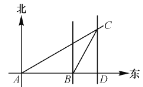
【题目】如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时30海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行1.5小时到达小岛C的正南方D点.求船从A到D一共走了多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
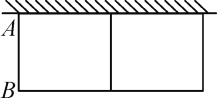
【题目】如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5m,墙外可用宽度为3.25m.现有长为21m的篱笆,计划靠着院墙围成一个中间有一道隔栏的长方形花圃.
(1)若要围成总面积为36m2的花圃,边AB的长应是多少?
(2)花圃的面积能否达到36.75m2?若能,求出边AB的长;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com