
设a=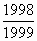 ,b=
,b= ,c=
,c=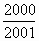 ,则下列不等式关系中,正确的是
,则下列不等式关系中,正确的是
[ ]
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源:2011河北省中考数学试题 题型:044
图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.

思考:如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α.
当α=________度时,点P到CD的距离最小,最小值为________.
探究一:在图1的基础上,以点M为旋转中心,在AB,CD之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO=________度,此时点N到CD的距离是________.
探究二:将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转.
(1)如图3,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.(参考数椐:sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分8分)
“6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B,
OB与小⊙O相交于点A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,
设∠FOB=α,OB=4,BC=6.
(1)求证:AD为小⊙O的切线;
 (2)在图中找出一个可用α表示的角,并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(2)在图中找出一个可用α表示的角,并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(3)当α=30º时,求DH的长。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2011届北京市门头沟区初三第一学期期末数学卷 题型:单选题
如图,在矩形ABCD中,AB=4,BC=3,点P在CD边上运动,联结AP,过点B作BE⊥AP,垂足为E,设AP= ,BE=
,BE= ,则能反映
,则能反映 与
与 之间函数关系的图象大致是
之间函数关系的图象大致是

查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市朝阳区初三第一学期期末数学卷 题型:选择题
如图,在矩形ABCD中,AB=4,BC=3,点P在CD边上运动,联结AP,过点B作BE⊥AP,垂足为E,设AP= ,BE=
,BE= ,则能反映
,则能反映 与
与 之间函数关系的图象大致是
之间函数关系的图象大致是
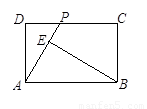

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
分析 (1)利用60°角![]() 的正弦值列式计算即可得解;
的正弦值列式计算即可得解;
(2)①连接CF并延长交BA的延长线于点G,利用“角边角”证明△AFG和△CFD全等,根据全等三角形对应边相等可得CF=GF,AG=CD,再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF,再根据A![]() B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,
B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,![]() 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
②设BE=x,在Rt△BCE中,利用勾股定理表示出CE2,表示出EG的长度,在Rt△CEG中,利用勾股定理表示出CG2,从而得到CF2,然后相减并整理,再根据二次函数的最值问题解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com