
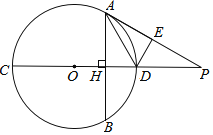
【题目】如图,CD为⊙O的直径,弦AB垂直于CD,垂足为H,∠EAD=∠HAD.
(1)求证:AE为⊙O的切线;
(2)延长AE与CD的延长线交于点P,过D 作DE⊥AP,垂足为E,已知PA=2,PD=1,求⊙O的半径和DE的长.
【答案】(1)见解析;(2)1.5,DE=![]()
【解析】
(1)连接OA,根据垂线的定义结合角的计算,即可得出∠EAD+∠OAD=90°,从而得出OA⊥AE,再由点A在圆上,即可证出AE为⊙O的切线;
(2)设⊙O的半径为x,在Rt△AOP中,利用勾股定理可求出x的值,再由DE⊥AP,得出OA∥DE,进而可得出△PED∽△PAO,根据相似三角形的性质即可求出DE的长度.
(1)证明:连结OA,如图所示.
∵AB⊥CD,
∴∠AHD=90°,
∴∠HAD+∠ODA=90°.
∵OA=OD,
∴∠OAD=∠ODA.
又∵∠EAD=∠HAD,
∴∠EAD+∠OAD=90°,
∴OA⊥AE.
又∵点A在圆上,
∵AE为⊙O的切线.
(2)解:设⊙O的半径为x,在Rt△AOP中,
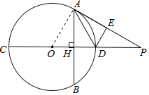
OA2+AP2=OP2,即x2+22=(x+1)2,
解得:x=1.5,
∴⊙O的半径为1.5.
∵DE⊥AP,OA⊥AP,
∴OA∥DE,
∴△PED∽△PAO,
∴![]() ,即
,即![]() ,
,
解得:DE=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
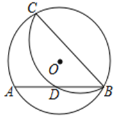
【题目】如图, 在⊙O 中,点 C 在优弧 AB 上, 将弧 BC 沿 BC 折叠后刚好经过 AB的中点 D. 若⊙O的半径为![]() ,AB=4,则 BC 的长是( )
,AB=4,则 BC 的长是( )
A.2![]() B.3
B.3![]() C.4D.2
C.4D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类是必须要落实的国家政策,环卫部门要求垃圾要按![]() 可回收物,
可回收物,![]() 有害垃圾,
有害垃圾,![]() 餐厨垃圾,
餐厨垃圾,![]() 其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).
其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).
(1)直接写出甲投放的垃圾恰好是![]() 类垃圾的概率;
类垃圾的概率;
(2)用树状图求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
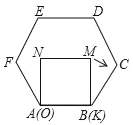
【题目】已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“ 亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
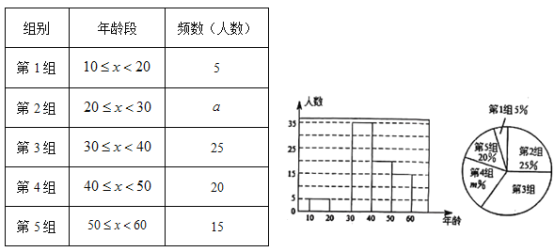
(1)请直接写出![]() _______,
_______,![]() _______,第3组人数在扇形统计图中所对应的圆心角是_______度.
_______,第3组人数在扇形统计图中所对应的圆心角是_______度.
(2)请补全上面的频数分布直方图.
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
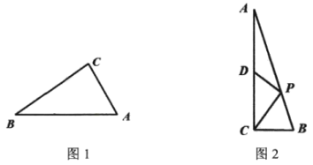
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:已知点![]() 是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点
是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点![]() 叫做该三角形的等距点.
叫做该三角形的等距点.
(1)如图1:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在斜边
在斜边![]() 上,且点
上,且点![]() 是
是![]() 的等距点,试求
的等距点,试求![]() 的长;
的长;
(2)如图2,![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 为
为![]() 中点,且
中点,且![]() .
.
①求证:![]() 的外接圆圆心是
的外接圆圆心是![]() 的等距点;②求
的等距点;②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=![]() (k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
(k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
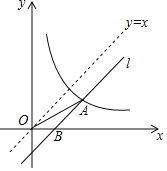
A.15B.5C.20D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com