
����Ŀ��������y=�� ![]() ��x��1��2+3��y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C��
��x��1��2+3��y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C��
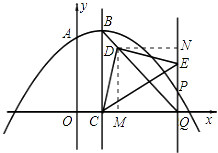
��1����ͼ1�����A�����꼰�߶�OC�ij���
��2����P���������ϣ�ֱ��PQ��BC��x���ڵ�Q������BQ��
������45��ǵ�ֱ�����ǰ���ͼ2��ʾ���ã����У�һ���������C�غϣ�ֱ�Ƕ���D��BQ�ϣ���һ������E��PQ�ϣ���ֱ��BQ�ĺ�������ʽ��
������30��ǵ�ֱ�����ǰ�һ���������C�غϣ�ֱ�Ƕ���D��ֱ��BQ�ϣ���һ������E��PQ�ϣ����P�����꣮
���𰸡�
��1��
�⣺��x=0���������ߵã�y= ![]() ��
��
���A��0�� ![]() ����
����
�����ߵĶԳ���Ϊx=1��
��OC=1
��2��
�⣺����ͼ��B��1��3��
�ֱ����D��DM��x����M��DN��PQ�ڵ�N��
��PQ��BC��
���DMQ=��DNQ=��MQN=90�㣬
���ı���DMQN�Ǿ��Σ�
�ߡ�CDE�ǵ���ֱ�������Σ�
��DC=DE����CDM=��EDN
�� 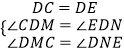 ��
��
���CDM�ա�EDN��AAS��
��DM=DN��
�����DMQN��������
���BQC=45��
��CQ=CB=3
��Q��4��0��
��BQ�Ľ���ʽΪ��y=kx+b��
��B��1��3����Q��4��0���������ʽ�ã�k=��1��b=4��
����ֱ��BQ�Ľ���ʽΪ��y=��x+4��
�ڵ���P�ڶԳ����Ҳ࣬��ͼ��
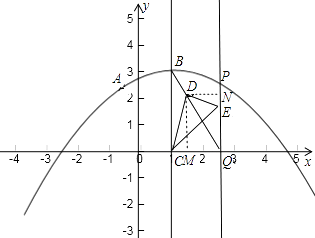
����D��DM��x����M��DN��PQ��N��
�ߡ�CDE=90�㣬���CDM=��EDN
���CDM�ס�EDN
����DCE=30�㣬 ![]() =
= ![]()
��DN=MQ
�� ![]() =
= ![]()
�� ![]() =
= ![]() ��BC=3��CQ=
��BC=3��CQ= ![]()
��Q��1+ ![]() ��0��
��0��
��P1��1+ ![]() ��
�� ![]() ��
��
����DCE=60�㣬��P2��1+3 ![]() ����
���� ![]() ����
����
����P�ڶԳ�������ʱ���ɶԳ���֪��
P3��1�� ![]() ��
�� ![]() ����P4��1��3
����P4��1��3 ![]() ����
���� ![]() ��
��
����������P1��1+ ![]() ��
�� ![]() ����P2��1+3
����P2��1+3 ![]() ����
���� ![]() ����P3��1��
����P3��1�� ![]() ��
�� ![]() ����P4��1��3
����P4��1��3 ![]() ����
���� ![]() ����
����
����������1����x=0�������������y��ֵȷ����A�����꣬��������ߵĶԳ���õ�OC�ij�����2�����ɡ�CDE�ǵ���ֱ�������Σ��ֱ����D��x���PQ�Ĵ��ߣ�ͨ��������ȫ�ȵõ���DQO=45�㣬�����Q�����꣬Ȼ���ô���ϵ�������BQ�Ľ���ʽ���ڷֵ�P�ڶԳ���������������ۣ����������������������Q�����꣬Ȼ����������������P�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ������߳�Ϊx�������οյأ������밴���ַ�ʽ��ֲ��Ƥ����ʽһ����ͼ�٣��������οյ�����������Ϊ2m��·��������ֲ��Ƥ����ʽ������ͼ�ڣ��������οյ����ܸ���һ��߳�Ϊm�������οյ�ֲ����������ֲ��Ƥ��ѧУ�����ַ�ʽ����5000Ԫ������Ƥ��

(1)д����ͼ���������ַ�ʽ�����Ƥ�ĵ��ۣ�
(2)��x��14��m��2ʱ�������ַ�ʽ�����Ƥ�ĵ��۸��Ƕ���(�������������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ˮ�ܵĽ�����ͼ��ʾ����֪��ˮ�ܵĽ���Բ�뾶OB=10������ԲԲ��O��ˮ��ľ���OC��6����ˮ���AB�ǣ� �� 
A.16
B.10
C.8
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������̼�������ѡ�������г���Ϊ�������ߣ���ͼ1��ʾ��һ�����г���ʵ��ͼ�����ܵ�AC��CD�ij��ֱ�Ϊ45cm��60cm�������ǻ��ഹֱ������CE�ij�Ϊ20cm����A��C��E��ͬһ��ֱ���ϣ��ҡ�CAB=75�㣬��ͼ2�� 
��1���ܵ�AD�ij���
��2��������E�����ܵ�AB�ľ��룮 �������ȷ�� 1cm���ο����ݣ�sin75���0.9659��cos75���0.2588��tan75��3.7321
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ��ʾ�����¿��е���Ŀ��
С����ͬ��С�����ۺ��������½��
��1���������̽������
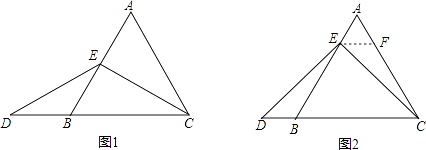
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�AEDB�����������������=������
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AEDB�����������������=�������������£�
��ͼ2������E��EF��BC����AC�ڵ�F��������������½����̣�
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC�ı߳�Ϊ1��AE=2����CD�ij�������ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����ADE�У���E��BC���ϣ���BAC����DAE����B����D�� AB��AD��
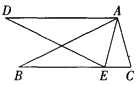
��1����˵����ABC�ա�ADE��
��2�������AEC��75��������ADE�Ƶ�A��תһ����Ǻ�����ABC�غϣ��������ת�ǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�л�����չ������������У�������Уѧ�����ÿ�����һСʱ��ijУ����ʵ�ʣ�������Ҫ����A��ƹ����B������C���ܲ���D�����������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ�����ͳ��ͼ��������ͼ����Ϣ����������⣮

��1���������ϲ��B��Ŀ��������ռ�İٷֱȣ�
��2�������D����������ͼ�е�Բ�ĽǵĶ�����
��3�����ͳ��ͼ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
(1)����ͼʾ��д�±���
ƽ����/�� | ��λ��/�� | ����/�� | |
AУ | ______ | 85 | ______ |
BУ | 85 | ______ | 100 |
(2)�����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
(3)������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��������һ����ABCֽƬ����D��E�ֱ��ڱ�AB��AC�ϣ��ֽ���ABC����DE�۵�ѹƽ��ʹ��A���ڵ�A��λ�ã�����A=75��������1+��2= ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com