
【题目】等边三角形的内切圆半径、外接圆半径和高的比为( )
A. 1∶![]() ∶
∶![]() B. 1∶2∶
B. 1∶2∶![]() C. 1∶
C. 1∶![]() ∶2 D. 1∶2∶3
∶2 D. 1∶2∶3
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
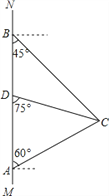
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有 4 个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于 4”的概率.
(3)梯形ABCD中,AB∥DC,∠B=90°,E 为直线 BC上一点,若AB=5,BC=12,DC=7,当BE=?时,△ABE与△DEC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 是反比例函数.
是反比例函数.
(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(![]() ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
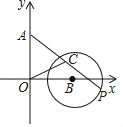
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.
求证:(1)DE⊥AE;
(2)AE+CE=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
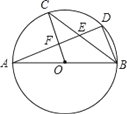
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com