练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，直线l经过A（3，0），B（0，3）两点，且与二次函数y=x2+1的图象，在第一象限内相交于点C．求：
    （1）△AOC的面积；
    （2）二次函数图象的顶点与点A、B组成的三角形的面积．
    （1）设直线AB的解析式为y=kx+b，
    把A（3，0），B（0，3）代入，得
    3k+b=0
    b=3
    ，
    解得
    k=-1
    b=3
    ，
    ∴直线AB：y=-x+3，
    解方程组
    y=x2+1
    y=-x+3
    ，
    得C（1，2），
    ∴△AOC的面积为
    1
    2
    ×3×2=3．

    （2）由顶点坐标公式得D（0，1），
    ∴S△ABD=
    1
    2
    ×2×3=3．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    已知抛物线y=-
    1
    2
    x2+mx+n    与x轴交于不同的两点A（x1，0），B（x2，0），点A在点B的左边，抛物线与y轴交于点C，若A，B两点位于y轴异侧，且tan∠CAO=tan∠BCO=
    1
    3
    ，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    抛物线y=x2+bx+c过点（2，-2）和（-1，10），与x轴交于A、B两点，与y轴交于C点．
    （1）求抛物线的解析式．
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    安庆迎江区农民张大伯为了致富奔小康，大力发展家庭养殖业，他准备用40米长的木栏围一个矩形的养圈，为了节约材料，同时要使矩形面积最大，他利用了自己家房屋一面长24米的墙，设计了如图一个矩形的养圈．
    （1）请你求出张大伯设计的矩形养圈的面积．
    （2）请你判断他的设计方案是否使矩形养圈的面积最大？如果不是最大，应怎样设计？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    进入三月以来，重庆的气温渐渐升高，羽绒服进入了销售淡季．为此重庆某百货公司对某品牌的A款羽绒服进行了清仓大处理．已知A款羽绒服的销售价格y元与第x天（1≤x≤10，且为整数）之间的关系可用如下表表示：
    时间（x天）12345678910
    售价y（元/件）550500450400350300300300300300
    在销售的前6天，A款羽绒服的销售数量z1（件）与第x天的关系式为z1=20x+40（1≤x≤6且为整数）；后4天（7≤x≤10，且为整数）的销售数量z2件与第x天的关系如图所示
    （1）请观察题中表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y与x之间的函数关系式，根据如图所示的变化趋势，直接写出z2与x之间的一次函数关系式．
    （2）若A款羽绒服的进价为每件200元，该专柜共有5个员工，每位员工每天的工资为100元，该专柜每天所需的固定支出为1000元，请结合上述信息，求这10天内哪天的利润最大，并求出这个最大利润．
    （3）在第（2）问的前提下，为了提高收益、减少库存，商场在第11天作出以下决定：第11-15天继续维持A款羽绒服的售价，结果每天的销售量均与第10天的持平，同时在第11-15天将B款羽绒服也作为促销商品，而且作为销售重点，已知B款羽绒服的进价仍为200元每件，销售价格比A款羽绒服取得最大利润当天的售价降低了a%，而每天销售量则比第10天A款羽绒服的销量提高了2a%，最后5天A、B两款羽绒服的总利润为27100元，请你参考以下数据，计算出a的值．
    参考数据：2.52=6.25，2.62=6.76，2.72=7.29，2.82=7.84．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是______cm2．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

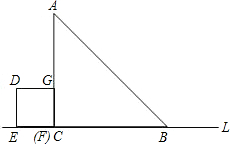    如图，在△ABC中，∠ACB=90°AC=BC=6cm，正方形DEFG的边长为2cm，其一边EF在BC所在的直线L上，开始时点F与点C重合，让正方形DEFG沿直线L向右以每秒1cm的速度作匀速运动，最后点E与点B重合．
    （1）请直接写出该正方形运动6秒时与△ABC重叠部分面积的大小；
    （2）设运动时间为x（秒），运动过程中正方形DEFG与△ABC重叠部分的面积为y（cm2）．
    ①在该正方形运动6秒后至运动停止前这段时间内，求y与x之间的函数关系式；
    ②在该正方形整个运动过程中，求当x为何值时，y=
    1
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在△ABC中，AB=BC=2，高BE=
    		3
    ，在BC边的延长线上取一点D，使CD=3．
    （1）现有一动点P由A沿AB移动，设AP=t，S△PCD=S，求S与t之间的关系式及自变量t的取值范围．
    （2）在（1）的条件下，当t=
    1
    3
    时，过点C作CH⊥PD于H，设K=7CH：9PD．求证：关于x的二次函数y=-x2-(10k-
    		3
    )x+2k    的图象与x轴的两个交点关于原点对称．
    （3）在（1）的条件下，是否存在正实数t，使PD边上的高CH=
    1
    2
    CD    ？如果存在，请求出t的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知：如图，Rt△AOB的两直角边OA、OB分别在x轴的正半轴和y轴的负半轴上，C为OA上一点且OC=OB，抛物线y=（x-2）（x-m）-（p-2）（p-m）（m、p为常数且m+2≥2p＞0）经过A、C两点．
    （1）用m、p分别表示OA、OC的长；
    （2）当m、p满足什么关系时，△AOB的面积最大．

    查看答案和解析>>

    同步练习册答案