
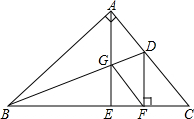
 如图,在△ABC中,∠BAC=90°,在BC上截取BF=BA,作DF⊥BC交AC于D点,AE⊥BC于E点,交BD于G点,连接GF,求证:DG平分∠AGF.
如图,在△ABC中,∠BAC=90°,在BC上截取BF=BA,作DF⊥BC交AC于D点,AE⊥BC于E点,交BD于G点,连接GF,求证:DG平分∠AGF. 分析 首先证得Rt△ABD≌Rt△FBD,得出∠ADB=∠FDB,AD=FD,再进一步证得△AGD≌△FGD,得出∠AGD=∠FGD证得结论.
解答 证明:∵∠BAC=90°,DF⊥BC,
∴在Rt△ABD≌Rt△FBD中,
$\left\{\begin{array}{l}{BD=BD}\\{BA=BF}\end{array}\right.$,
∴Rt△ABD≌Rt△FBD,
∴∠ADB=∠FDB,AD=FD,
在△AGD和△FGD中,
$\left\{\begin{array}{l}{AD=DF}\\{∠ADG=∠FDG}\\{DG=DG}\end{array}\right.$,
∴△AGD≌△FGD,
∴∠AGD=∠FGD,
即DG平分∠AGF.
点评 此题考查三角形全等的判定与性质,掌握三角形全等的判定方法是解决问题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
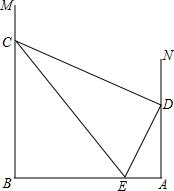 如图,过线段AB两端点分别作MB⊥AB,NA⊥AB,垂足分别为点B、点A;点D是射线AN上的-点,点E是线段AB上的一动点,联结DE,过点D作DC⊥DE,与射线BM交于点C,联结CE;
如图,过线段AB两端点分别作MB⊥AB,NA⊥AB,垂足分别为点B、点A;点D是射线AN上的-点,点E是线段AB上的一动点,联结DE,过点D作DC⊥DE,与射线BM交于点C,联结CE;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
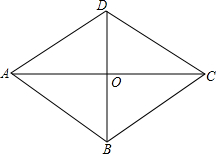 如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:
如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
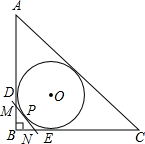 如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D,E,如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为2,则Rt△MBN的周长为4.
如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D,E,如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为2,则Rt△MBN的周长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com