【题目】如图，已知
的平分线与
的垂直平分线相交于点
，
，
，垂足分别为
，
，
，
，则
的长为__________．
【答案】
【解析】
连接DC、DB，根据中垂线的性质即可得到DB=DC，根据角平分线的性质即可得到DE=DF，从而即可证出△DEB≌DFC，从而得到BE=CF，再证△AED≌△AFD，即可得到AE=AF，最后根据
，
即可求出BE.
解：如图所示，连接DC、DB，
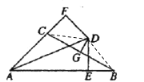
∵DG垂直平分BC
∴DB=DC
∵AD平分
，
，
∴DE=DF，∠DEB=∠DFC=90°
在Rt△DEB和Rt△DFC中，
∴Rt△DEB≌Rt△DFC
∴BE=CF
在Rt△AED和Rt△AFD中，
∴Rt△AED≌Rt△AFD
∴AE=AF
∴AB=AE＋BE=AF＋BE=AC＋CF＋BE=AC＋2BE
∵，
∴BE=
（AB－AC）=1.5.
故答案为：1.5.
科目：初中数学 来源： 题型：
【题目】对于抛物线
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解
如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
探究发现
△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ （填“是”或“不是”）．
小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
应用提升
（3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A（4,0），点B（0,6），点P是直线AB上的一个动点，已知点P的坐标为（m,n）.
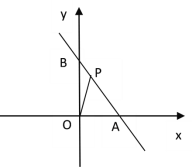
(1)当点P在线段AB上时（不与点A、B重合）
①当m=2,n=3时，求△POA的面积.
②记△POB的面积为S，求S关于m的函数解析式，并写出定义域.
（2）如果S△BOP：S△POA=1:2,请直接写出直线OP的函数解析式.（本小题只要写出结果，不需要写出解题过程）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：关于x的二次函数
的图象与x轴交于点A(1，0)和点B，与y轴交于点C(0，3)，抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式；
(2)在y轴上是否存在一点P，使△PBC为等腰三角形.若存在，请求出点P的坐标；
(3)有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到 达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长方形
中，
，
，点
从点
出发，以
的速度沿
向点
运动，设点的运动时间为
秒：
（1）
________
;(用的代数式表示)
（2）当为何值时，
≌
；
（3）当点从点开始运动，同时，点
从点出发，以
的速度沿
向点
运动，是否存在这样的
值，使得与
全等？若存在，请求出的值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
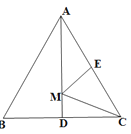
【题目】如图，等边△ABC的边长为2，AD是BC边上的中线，M是AD上的动点，E是边AC的中点，则EM+CM的最小值为( )
A.1B.12 C.3 D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α等于( )
A. 20° B. 30° C. 40° D. 50°
查看答案和解析>>
科目：初中数学 来源： 题型：
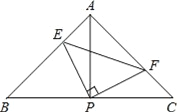
【题目】如图已知在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB和AC于点E、F，给出以下五个结论正确的个数有（ ）
①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），S四边形AEPF=
S△ABC．
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com