
分析 根据分式的减法和除法可以化简题目中的式子,然后选取一个使得原分式有意义的x的值代入求值即可,注意整数x满足-$\sqrt{5}$$<x<\sqrt{7}$.
解答 解:($\frac{2x}{x+2}$-$\frac{x}{x-2}$)÷$\frac{x}{{x}^{2}-4}$
=$\frac{2x(x-2)-x(x+2)}{(x+2)(x-2)}•\frac{(x+2)(x-2)}{x}$
=2(x-2)-(x+2)
=2x-4-x-2
=x-6,
∵x满足-$\sqrt{5}$$<x<\sqrt{7}$,
∴当x=1时,原式=1-6=-5.
点评 本题考查分式的化简求值、估算无理数的大小,解答本题的关键是明确分式化简求值的方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
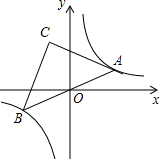 如图,在反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,若tan∠CAB=2,则k的值为( )| A. | -3 | B. | -6 | C. | -9 | D. | -12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
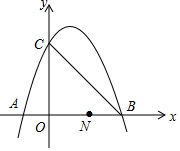 如图,已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )| A. | ($\frac{9}{2}$,$\frac{3}{2}\sqrt{7}$) | B. | ($\frac{21}{2}$,$\frac{3}{2}\sqrt{7}$) | C. | ($\frac{21}{2}$,$\frac{3}{2}\sqrt{5}$) | D. | ($\frac{25}{2}$,$\frac{3}{2}$$\sqrt{5}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
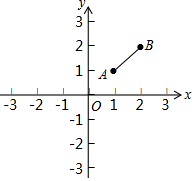 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )| A. | k>0 | B. | k≥1 | C. | k≥4 | D. | 1≤k≤4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
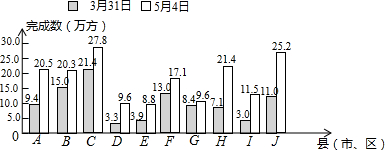
| 县(市、区) | 任务数(万方) |
| A | 25 |
| B | 25 |
| C | 20 |
| D | 12 |
| E | 13 |
| F | 25 |
| G | 16 |
| H | 25 |
| I | 11 |
| J | 28 |
| 合计 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.77×105 | B. | 47.7×105 | C. | 4.77×106 | D. | 0.477×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com