
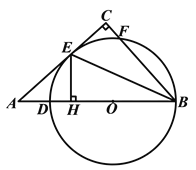
【题目】如图,在△![]() 中,∠
中,∠![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 相切于点
相切于点![]() ,与边
,与边![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)连接OE.由切线的性质得到OE⊥AC,从而有OE∥BC,由平行线的性质得到∠OEB=∠CBE.再由等腰三角形的性质得到∠OEB=∠OBE,即有∠OBE=∠CBE,由角平分线的性质即可得出结论;
(2)解Rt△ABC得到AB的长.再由OE∥BC,得到△AEO∽△ACB,由相似三角形对应边成比例,得到OB的长,进而可得出结论.
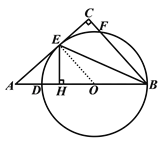
详解:(1)连接OE.
∵⊙O与边AC相切,∴OE⊥AC.
∵∠C=90°,∴OE∥BC,∴∠OEB=∠CBE.
∵OB=OE,∴∠OEB=∠OBE,∴∠OBE=∠CBE.
∵EH⊥AB,∴EH=EC.
(2)在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ∥
∥![]() ,∴△AEO∽△ACB,
,∴△AEO∽△ACB,
∴![]() ,即
,即![]() .
.
解得:![]() ,
,
∴![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
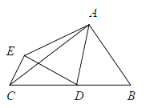
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
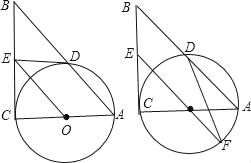
【题目】【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为![]() .
.
(1)求反比例函数的表达式;
(2)设直线![]() 与
与![]()
![]() 轴,
轴,![]() 轴分别交于点C,D,且
轴分别交于点C,D,且![]() ,直接写出
,直接写出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
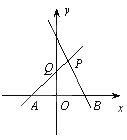
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
(1)已知,点![]() ,
,
①点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
②点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
(2)若点P在![]() 轴上,且点P的“伴随圆”与直线
轴上,且点P的“伴随圆”与直线![]() 相切,求点P的坐标;
相切,求点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M、N是BC、CD边上的点,连接AM、BN,若BM=CN

(1)求证:AM⊥BN
(2)将线段AM绕M顺时针旋转90°得到线段ME,连接NE,试说明:四边形BMEN是平行四边形;
(3)将△ABM绕A逆时针旋转90°得到△ADF,连接EF,当![]()
![]() 时,请求出
时,请求出![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一四柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供的信息,解答下列问题:
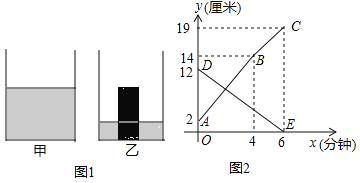
(1)图2中折线ABC表示 槽中水的深度与注水时间关系,线段DE表示 槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙.两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),则乙槽中铁块的体积为 立方厘米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com