
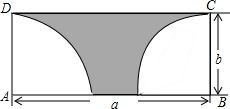
 如图所示,长方形ABCD的长是a,宽为b,分别以A,B为圆心,b为半径作扇形,用代数式表示阴影部分的周长C和面积S.
如图所示,长方形ABCD的长是a,宽为b,分别以A,B为圆心,b为半径作扇形,用代数式表示阴影部分的周长C和面积S. 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
 3、如图所示,长方形花园ABCD中,AB=a,AD=b,花园中建有一条长方形道路LMPQ及一条平行四边形道路RSTK,若LM=RS=c,则花园中可绿化部分的面积为
3、如图所示,长方形花园ABCD中,AB=a,AD=b,花园中建有一条长方形道路LMPQ及一条平行四边形道路RSTK,若LM=RS=c,则花园中可绿化部分的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )
某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )| A、1:2 | B、2:3 | C、2:5 | D、3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
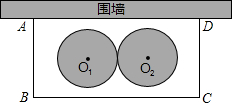 某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:
 弹子盘为长方形ABCD,四角有洞,弹子从A出发,路线与小正方形的边成45°角,撞到边界即反弹(如图所示).AB=4,AD=3,弹子最后落入B洞.那么,当AB=9,AD=8时,弹子最后落入
弹子盘为长方形ABCD,四角有洞,弹子从A出发,路线与小正方形的边成45°角,撞到边界即反弹(如图所示).AB=4,AD=3,弹子最后落入B洞.那么,当AB=9,AD=8时,弹子最后落入查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com