
分析 (1)先化简二次根式,再计算即可;
(2)根据x,y的值,先提公因式,再计算即可.
解答 解:(1)原式=(40$\sqrt{3}$-18$\sqrt{3}$+8$\sqrt{3}$)÷$\sqrt{6}$
=30$\sqrt{3}$÷$\sqrt{6}$
=15$\sqrt{2}$;
(2)∵x=$\sqrt{3}-\sqrt{2}$,y=$\sqrt{3}+\sqrt{2}$,
∴x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
=($\sqrt{3}-\sqrt{2}$)($\sqrt{3}+\sqrt{2}$)[($\sqrt{3}-\sqrt{2}$+$\sqrt{3}+\sqrt{2}$)2-2($\sqrt{3}-\sqrt{2}$)($\sqrt{3}+\sqrt{2}$)]
=(2$\sqrt{3}$)2-2
=12-2
=10.
点评 本题考查了二次根式的化简求值以及分母有理化,掌握化二次根式为最简二次根式是解题的关键.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
 如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求:
如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5厘米 | B. | 10厘米 | C. | 15厘米 | D. | 20厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
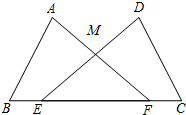 如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )| A. | ∠B | B. | ∠A | C. | ∠EMF | D. | ∠AFB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com