
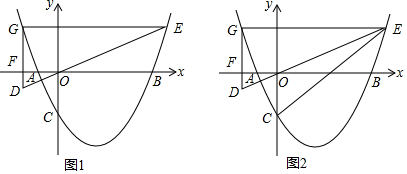
分析 (1)令y=0求出A、B两点坐标,即可求出AB的值.
(2)想办法求出E、G、D坐标,即可求出GF、DF,由此即可解决问题.
(3)如图3中,设EG交y轴于M,由∠ECO=45°,EG⊥CM,推出∠MCE=∠MEC=45°,EM=MC=6,12a=6,推出a=$\frac{1}{2}$,可得F(-2,0),D(-2,-1),E(6,3),抛物线的解析式为y=$\frac{1}{2}$(x-2)2-5,即y=$\frac{1}{2}$x2-2x-3,设P(m,$\frac{1}{2}$m2-2m-3),根据S△PRD-S△PRO=S△EFD,列出方程即可解决问题.
解答 解:(1)对于抛物线y=a(x-2)2-10a,令y=0得到a(x-2)2-10a=0,
解得x=2±$\sqrt{10}$,
∴B(2+$\sqrt{10}$,0),A(2-$\sqrt{10}$,0),
∴AB=2+$\sqrt{10}$-2+$\sqrt{10}$=2$\sqrt{10}$.
(2)如图1中,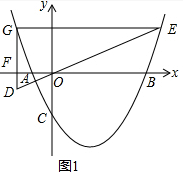
∵直线y=kx与抛物线y=a(x-2)2-10a交于点E,点E的横坐标为6,
∴E(6,6a),
把E(6,6a)代入y=kx得到k=a,
∴直线的解析式为y=ax,
∵点E、G关于直线x=2对称,
∴G(-2,6a),
∵GD∥y轴,
∴D(-2,-2a),
∴GF=6a,DF=2a,
∴GF=3DF.
(3)如图3中,设EG交y轴于M,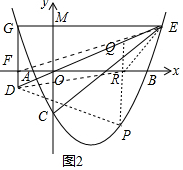
由题意,C(0,-6a),M(0,6a),
∵∠ECO=45°,EG⊥CM,
∴∠MCE=∠MEC=45°,
∴EM=MC=6,
∴12a=6,
∴a=$\frac{1}{2}$,
∴F(-2,0),D(-2,-1),E(6,3),抛物线的解析式为y=$\frac{1}{2}$(x-2)2-5,即y=$\frac{1}{2}$x2-2x-3,
设P(m,$\frac{1}{2}$m2-2m-3),
∵S△PRD-S△PRO=S△EFD,
∴$\frac{1}{2}$•(m+2)•(-$\frac{1}{2}$m2+2m+3)-$\frac{1}{2}$•m•(-$\frac{1}{2}$m2+2m+3)=$\frac{1}{2}$•1•8,
整理得m2-4m-2=0,解得m=2+$\sqrt{6}$或2-$\sqrt{6}$(舍弃),
∴点P坐标为(2+$\sqrt{6}$,-2).
点评 本题考查二次函数综合题、待定系数法、等腰直角三角形的性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数,构建方程,学会用转化的思想思考问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
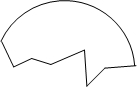 一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此件文物进行复原,如图所示,请你帮助文物学家作出此文物轮廓圆心O的位置(要求:尺规作图,保留作图痕迹,不写作法).
一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此件文物进行复原,如图所示,请你帮助文物学家作出此文物轮廓圆心O的位置(要求:尺规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{12}$=4$\sqrt{3}$ | C. | $\sqrt{3}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000(1+x)2=1440 | B. | 1000(x2+1)=1440 | ||
| C. | 1000+1000x+1000x2=1440 | D. | 1000+1000(1+x)+1000(1+x)2=1440 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com