
| A. | $\frac{1}{32}$ | B. | 1-$\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | 1-$\frac{1}{16}$ |
分析 根据题意可以求出每次剩下的蛋糕,从而可以解答本题.
解答 解:由题意可得,
第一天剩下:1-$\frac{1}{2}$=$\frac{1}{2}$,
第二天剩下:$\frac{1}{2}-\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$,
第三天剩下:$\frac{1}{4}-\frac{1}{4}×\frac{1}{2}$=$\frac{1}{8}$,
第四天剩下:$\frac{1}{8}-\frac{1}{8}×\frac{1}{2}=\frac{1}{16}$,
第五天剩下:$\frac{1}{16}-\frac{1}{16}×\frac{1}{2}$=$\frac{1}{32}$,
故选A.
点评 本题考查有理数的乘方,解题的关键是明确题意,算出每次剩下的蛋糕数.


科目:初中数学 来源: 题型:选择题
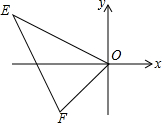 在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )
在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,4) | C. | (2,-1) | D. | (8,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 操作探究:
操作探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{pv}{1+2p}$ | B. | $\frac{pv}{1-2p}$ | C. | $\frac{pv}{2p-1}$ | D. | $\frac{v-2}{p}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com