
| 平板电脑 | PC机 | |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
分析 (1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,根据题意可得等量关系:公司获得的利润y=平板电脑x台的利润+PC机(30-x)台的利润,根据等量关系可得函数关系式;
(2)根据资金12.8万元和利润不少于1.5万元列出不等式组$\left\{{\begin{array}{l}{5400x+3500({30-x})≤128000}\\{300x+12000≥15000}\end{array}}\right.$,再解即可;
(3)根据一次函数的性质:k>0时,y随x的增大而增大可得答案.
解答 解:(1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,
根据题意得:y=(6100-5400)x+(3900-3500)(30-x),
整理得:y=300x+12000;
(2)由题意得:$\left\{{\begin{array}{l}{5400x+3500({30-x})≤128000}\\{300x+12000≥15000}\end{array}}\right.$,
解之得:$10≤x≤12\frac{2}{19}$,
∴整数x=10,11,或12;
所以该公司共有3种进货方案可供选择:
方案一:购进平板电脑10台,PC机20台;
方案二:购进平板电脑11台,PC机19台;
方案三:购进平板电脑12台,PC机18台;
(3)∵对于函数y=300x+12000,y随x的增大而增大,
∴该公司选择方案三:购进平板电脑12台,PC机18台.能获得最大利润,
此时,最大利润y=300×12+12000=15600 (元).
点评 此题主要考查了一次函数的应用,关键是正确理解题意,找出等量关系,列出函数关系式.


科目:初中数学 来源: 题型:解答题
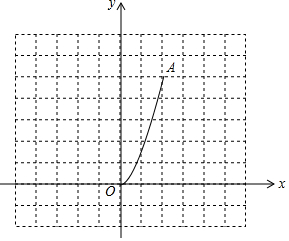 如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.
如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
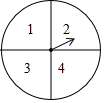 元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com