
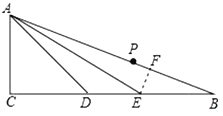
【题目】如图,![]() 中
中![]() 且
且![]() ,又
,又![]() 、
、![]() 为
为![]() 的三等分点.
的三等分点.

(1)求证![]() ;
;
(2)证明:![]() ;
;
(3)若点![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() 则使线段
则使线段![]() 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由)
【答案】(1)见解析;(2)见解析;(3)4.
【解析】
(1)利用勾股定理求得AD、DE的长,再根据BD、AD的长,利用两边对应相等,且夹角相等的两个三角形相似,即可判断;
(2)利用相似三角形的对应角相等以及三角形的外角的性质即可判断;
(3)作EF⊥AB于点F,利用△ABC∽△EBF,求得EF的长,即可确定PE的长的范围,从而求解.
解:(1)证明:∵![]() ,
,
∴![]() ,
,
∴在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(2)证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)作![]() 于点
于点![]() .
.
在直角![]() 中,
中,![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() .
.
又∵![]() ,
,![]()
![]() ,
,
则![]() ,
,![]() 的整数值是1或2或3.
的整数值是1或2或3.
则当![]() 时,
时,![]() 的位置有2个;
的位置有2个;
当![]() 时,
时,![]() 的位置有1个;
的位置有1个;
当![]() 时,
时,![]() 的位置有1个.
的位置有1个.
故![]() 的整数点有4个.
的整数点有4个.
故答案是:4.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.
(1)在图1中,DE交AB于M,DF交BC于N.
①求证:DM=DN;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(2)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:

(1)扇形统计图中a的值为 ;
(2)补全频数分布直方图;
(3)在这次抽样调查中,众数是 天,中位数是 天;
(4)请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】9月6日,重庆来福购物中心正式开业,购物中心里的美食店推出了A、B两种套餐和其他美食,当天,A套餐的销售额占总销售额的40%,B套餐的销售额占总销售额的20%,国庆期间,重庆外来旅客增加,此店老板考虑外来游客的饮食口味推出了C套餐,在10月1日这一天,A、B套餐各自的销售额都比9月6日的销售额减少了15%,C套餐的销售额占10月1日当天总销售额的20%,其他美食的销售额不变,则10月1日的总销售额比9月6日的总销售额增加__________%.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,点B是数轴上在A点左侧的一点,且A、B两点间的距离为10,动点P从点A出发,以每秒3个单位长度的速度沿数轴向左运动.
![]()
(1)数轴上点B表示的数是 ;
(2)运动1秒时,点P表示的数是 ;
(3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?相遇时对应的有理数是多少?
②当点P运动多少秒时,点P与点Q的距离为8个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com