【题目】如图，一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN．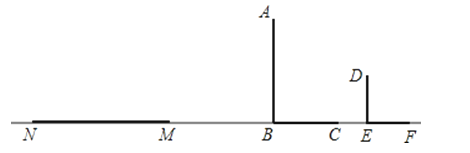
（1）试判断是路灯还是太阳光产生的影子，如果是路灯产生的影子确定路灯的位置（用点P表示）．如果是太阳光请画出光线．
（2）在图中画出表示大树高的线段．
科目：初中数学 来源： 题型：
【题目】甲、乙两列火车分别从A，B两城同时相向匀速驶出，甲车开往终点B城，乙车开往终点A城，乙车比甲车早到达终点；如图，是两车相距的路程d（千米）与行驶时间t（小时）的函数关系图象．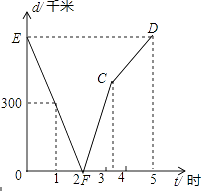 
（1）A，B两城相距千米，经过小时两车相遇；
（2）分别求出甲、乙两车的速度；
（3）直接写出甲车距A城的路程S1、乙车距A城的路程S2与t的函数关系式；（不必写出t的范围）
（4）当两车相距100千米时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
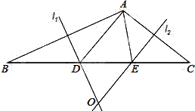
【题目】如图，在△ABC中，AB边的垂直平分线
交BC于D，AC边的垂直平分线
交BC于E， 
与
相交于点O，△ADE的周长为6cm．
（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题引入：
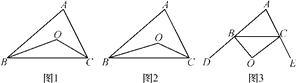
(1)如图1，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A＝α，则∠BOC＝ (用α表示)；
如图2，∠CBO＝
∠ABC，∠BCO＝∠ACB，∠A＝α，则∠BOC＝ (用α表示)；
拓展研究：
(2)如图3，∠CBO＝∠DBC，∠BCO＝∠ECB，∠A＝α，猜想∠BOC＝ (用α表示)，并说明理由；
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO＝
∠DBC，∠BCO＝∠ECB，∠A＝α，请猜想∠BOC＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国有五座名山，但在洪雅人的心目中，我国有六座名山，这六座名山的海拔分别为：
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔（米） | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
（1）海拔最高的山是多少，最高的山与最低的山的海拔相差多少米；
（2）海拔不低于1500米的山的频数是多少；频率是多少；
（3）根据数据制作条形统计图．
查看答案和解析>>
科目：初中数学 来源： 题型：
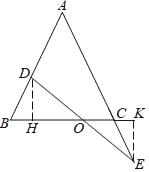
【题目】如图，△ABC中，AB=AC，D、E分别是AB及AC延长线上的点，且BD=CE，连接DE交BC于点O．过点D作DH⊥BC，过E作EK⊥BC，垂足分别为H、K．
（1）求证：DH=EK；
（2）求证：DO=EO．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．
（1）求OC的长；
（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；
（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知直线
与x、y轴交于B、C两点，A（0，0），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第n个等边三角形的边长等于（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
