
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F, 连结AF,BE相交于点P.
(1)若AE=CF.
①求证:AF=BE,并求∠APB的度数.
②若AE=2,试求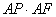 的值.
的值.
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.

 (1)①如图,∵△ABC是等边三角形,
(1)①如图,∵△ABC是等边三角形,
∴∠C=∠BAC=60°, AB=AC,
又∵AE=CF,
∴△AFC≌△BEA (SAS),
∴AE=CF,
∠1=∠3,
∵∠4=∠2+∠3,
∴∠4=∠2+∠1=∠BAC=60°,
即∠ APB=180°-∠4=120°.
APB=180°-∠4=120°.
 ② ∵ ∠C=∠4=60°,∠PAE=∠CAF,
② ∵ ∠C=∠4=60°,∠PAE=∠CAF,
∴ △APE∽△ACF,
∴ ,即
,即 ,所以
,所以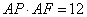 .
.
(2)若AF=BE,有AE=BF或AE=CF两种情况.
当AE=BF时,如图2,此时点P经过的路径是AB边上的高线CH.
在Rt△AHC中, ,
,
∴此时点P经过的路径长为
 .
.
当AE=CF时,如图3,点P经过的路径是以A,B为端点的 圆弧,且∠APB=120°,则圆心角∠AOB=120°,
 过点O作OG⊥AB, 在Rt△AOG中,∠AOG=60°,
过点O作OG⊥AB, 在Rt△AOG中,∠AOG=60°,
 ,
,
∴ .
.
∴此时点P经过的路径长为 .
.
所以,点P经过的路径长为 或
或 .
.


科目:初中数学 来源: 题型:
某市6月份某周气温(单位:℃)为23、25、28、25、28、31、28,则这组数据的众数和中位数分别是( )
|
| A. | 25、25 | . | 28、28 | C. | 25、28 | D. | 28、31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
图①是电子屏幕的局部示意图,4×4网格的每个小正方形边长均为1,每个小正方形顶点叫做格点,点A,B,C,D在格点上,光点P从AD的中点出发,按图②的程序移动
(1)请在图①中用圆规画出光点P经过的路径;
(2)在图①中,所画图形是 图形(填“轴对称”或“中心对称”),所画图形的周长是 (结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com