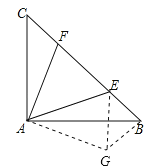
【题目】如图，在等腰直角△ABC的斜边上取异于B，C的两点E，F，使∠EAF=45°，求证：以EF，BE，CF为边的三角形是直角三角形．
【答案】证明见解析.
【解析】试题分析：首先把△ACF绕点A顺时针旋转90°，得到△ABG．连接EG，可得△ACF≌△ABG．进而得到AG=AF，BG=CF，∠ABG=∠ACF=45°，再证明△AEG≌△AEF可得EF=EG，由∠GBE=90°利用勾股定理可得BE2+CF2=EF2，那么根据勾股定理的逆定理得出以EF，BE，CF为边的三角形是直角三角形．
试题解析：证明：把△ACF绕点A顺时针旋转90°，得到△ABG．连接EG．则△ACF≌△ABG，∴AG=AF，BG=CF，∠ABG=∠ACF=45°．∵∠BAC=90°，∠GAF=90°，∴∠GAE=∠EAF=45°．在△AEG和△AEF中，∵
，∴△AEG≌△AEF（SAS），∴EG=EF．又∵∠GBE=90°，∴BE2+BG2=EG2，即BE2+CF2=EF2，∴以EF，BE，CF为边的三角形是直角三角形．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在有些情况下，不需要计算出结果也能把绝对值符号去掉．例如：
|6＋7|＝6＋7；|6－7|＝7－6；|7－6|＝7－6；|－6－7|＝6＋7；
根据上面的规律，把下列各式写成去掉绝对值符号的形式：
(1)|7－21|＝_________；
(2)|
|＝____________；
(3)|
|＝__________；
(4)用合理的方法计算：|
|＋|
|－
×|－|＋
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE．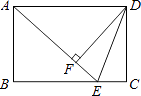 
（1）求证：AB=DF；
（2）若AD=10，AB=6，求tan∠EDF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门随机调查了某单位员工上下班的交通方式，绘制了如下统计图，根据统计图，完成下列问题：
（1）调查的总人数为 ；
（2）补全条形统计图；
（3）该单位共有2000人，为了积极践行“低碳生活，绿色出行”这种生活方式，调查后开私家车的人上下班全部改为骑自行车，则现在骑自行车的人数约为多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的文字，解答问题.
大家知道
是无理数，而无理数是无限不循环小数，因此
的小数部分我们不可能全部地写出来，但是由于1＜
＜2，所以
的整数部分为1，将
减去其整数部分1，差就是小数部分
-1，根据以上的内容，解答下面的问题：
（1）
的整数部分是 ，小数部分是 ；
（2）1+
的整数部分是 ，小数部分是 ；
（3）若设2+
整数部分是x，小数部分是y，求x-y的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列哪组条件能够判别四边形ABCD是平行四边形？（ ）
A. AB∥CD，AD＝BC B. AB＝CD，AD＝BC
C. ∠A＝∠B，∠C＝∠D D. AB＝AD，CB＝CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
