
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 |
| 决赛成绩(单位:分) | ||||||||||
| 初一年级 | 80 | 86 | 88 | 80 | 88 | 99 | 80 | 74 | 91 | 89 |
| 初二年级 | 85 | 85 | 87 | 97 | 85 | 76 | 88 | 77 | 87 | 88 |
| 初三年级 | 82 | 80 | 78 | 78 | 81 | 96 | 97 | 88 | 89 | 86 |
| 平均数 | 众数 | 中位数 | |
| 初一年级 | 85.5 | 80 | |
| 初二年级 | 85.5 | 86 | |
| 初三年级 | 84 |
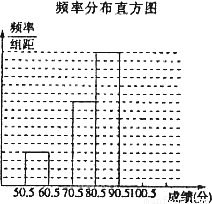
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | 0.24 |
| 合计 |
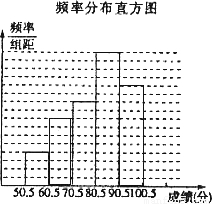
| 平均数 | 众数 | 中位数 | |
| 初一年级 | 85.5 | 80 | 88 |
| 初二年级 | 85.5 | 85 | 86 |
| 初三年级 | 85.5 | 78 | 84 |


科目:初中数学 来源:2010年中考数学考前10日信息题复习题精选(5)(解析版) 题型:解答题
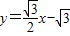 上.
上.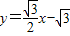 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;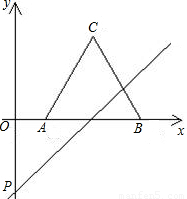
查看答案和解析>>
科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题
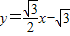 上.
上.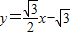 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;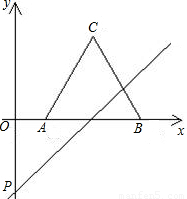
查看答案和解析>>
科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题
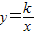 的图象经过点(-1,3)
的图象经过点(-1,3)查看答案和解析>>
科目:初中数学 来源:2006年湖南省湘潭市中小学教师业务理论考试初中数学试卷(解析版) 题型:解答题
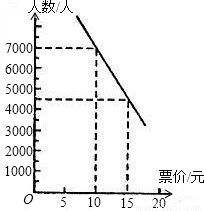
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com