
����Ŀ����ͼ1����֪������ABCD��AB=CD�� BC=AD��PΪ������ABCD���ϵĶ���������P��A����������A��B��C��D�˶���D��ֹͣ���ٶ�Ϊ2cm/s�����P�õ�ʱ��Ϊx������APD�����Ϊy![]() ��y��x�Ĺ�ϵ��ͼ2��ʾ.
��y��x�Ĺ�ϵ��ͼ2��ʾ.

��1��AB=________cm, BC=______cm;
��2��д��![]() ʱ,y��x֮��Ĺ�ϵʽ��
ʱ,y��x֮��Ĺ�ϵʽ��
��3����y=12ʱ����x��ֵ��
��4����P���߶�BC���˶�ʱ���Ƿ���ڵ�Pʹ����APD���ܳ���С�������ڣ������ʱ��APD�Ķ������������ڣ���˵�����ɣ�
���𰸡���1��AB=6cm��BC=12cm����2��y=12x����3��x=1��11����4�����ڣ���ʱ��APD =90��
����������1�����ݺ���ͼ��ɵô�A��B������3�룬��B��C����6�룬�ٶ�Ϊ2cm/s,��ɼ����AB��BC�ij��ȣ�
��2���������������ʽ�ɵ�: ����APD�����=![]() ��AP��2x�ɵó�y��x֮��Ĺ�ϵʽ��
��AP��2x�ɵó�y��x֮��Ĺ�ϵʽ��
��3����������ۣ�����P��AB��CD��ʱ�����x��ֵ����;
��4����A����ֱ��BC�ĶԳƵ�A�䣬����A��D��BC���ڵ�P����������֮�ʹ��ڵ����߿�֪A��D��С������APD���ܳ���С�������APD=��A��+��BAP=90�㣮
��1�����ɺ���ͼ��ɵã���P��A��B������3�룬��B��C����6�룬��P���ٶ�Ϊ2cm/s
��AB=6cm, BC=12cm;
��2����ͼ��ʾ��
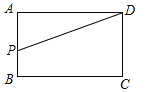
��![]() ʱ,��P���߶�AB�ϣ�AP��2x,
ʱ,��P���߶�AB�ϣ�AP��2x,
��S��ADP=![]() .
.
��3����ͼ��ʾ��
�����������
�ٵ�P��AB��ʱ����ͼ��ʾ����y=3ʱ��3=3x��x=1��

�ڵ�P��CD��ʱ����ͼ��ʾ����AB+BC+CP=t��
��PD=3+3+6-t=12-t��
��y=![]() PDAD=
PDAD=![]() ��6����12-t��=3��12-t����
��6����12-t��=3��12-t����
��y=3ʱ��3=3��12-t����
t=11��
������������y=3ʱ��x��ֵ��1���11�룻
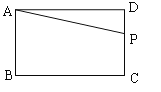
��4�����ڣ���ͼ��ʾ���ӳ�AB��A�䣬ʹAB=A��B������A��D����BC��P������AP��
��ʱ��APD���ܳ���С��
��AA��=AB+BA��=3+3=6��
��AD=AA��=6��
���A��AD�ǵ���ֱ�������Σ�
���A��=45�㣬
�ߡ�ABC=90�㣬
��BP��AA����д��ߣ�
��AP=PA�䣬
���A��=��BAP=45�㣬
���APD=��A��+��BAP=90�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���A������Ϊ(2��4)����B������Ϊ(2��7) ��ֱ��l����A����ƽ����x
�ᣬֱ��l�ϵĶ���C��A�������ÿ��4����λ���ٶ���ֱ��l�˶�������x����������D��E,
����DB��OB������EC��OC������DB��OB��EC��OC�����C�˶�ʱ��t�룬
(1) ��ͼ1��������C��A����������˶�����t��1��ʱ��
�����߶�BC�ij��͵�E�����ꣻ
�����ʱDE��AC��������ϵ��
(2)̽��������C��ֱ��l�˶�������tȡ��ֵ���Ƿ���������1�����е�������ϵ�� �����ڣ���֤�����������ڣ���˵������.


ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA=2��OC=6����OC��ȡ��D����AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦����һ���㹻���ֱ�����ǰ�Ķ���P��D��������߶�DA��AB�ƶ�����һֱ�DZ�ʼ�վ�����D����һֱ�DZ�����ֱ����ֱ��DE��BC�ֱ��ڵ�M��N��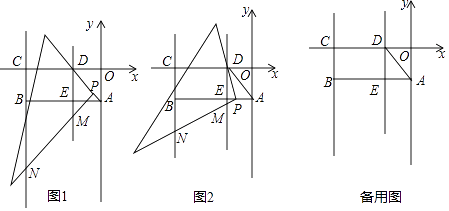
��1����գ�����A��B��D����������ߵĽ���ʽ����
��2����֪��F�ڣ�1���е������ߵĶԳ����ϣ����F����B��D�ľ���֮������ֵ��
��3����ͼ1������P���߶�DA���ƶ�ʱ���Ƿ���������ĵ�M��ʹ��CMNΪ���������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��4����ͼ2������P���߶�AB���ƶ�ʱ����P������Ϊ��x����2�����ǡ�DBN�����ΪS����ֱ��д��S��x֮��ĺ�����ϵʽ�������S��x���������ʱ����Ӧ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��AB=10����AC=6����BAC��ƽ���߽���O�ڵ�D������D��DE��AC��AC���ӳ����ڵ�E�� 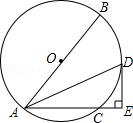
��1����֤��DE�ǡ�O�����ߣ�
��2����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AΪ���� ![]() ͼ����һ�㣬����OA��������
ͼ����һ�㣬����OA�������� ![]() ��ͼ���ڵ�B����C��x����һ�㣬��AO=AC�����ABC�������
��ͼ���ڵ�B����C��x����һ�㣬��AO=AC�����ABC������� 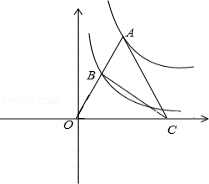
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��̽������ͼ����ֱ��AB��BC��AC�����ཻ������ֱ�Ϊ��A��B��C����D���߶�AB��������D��DE��BC��AC�ڵ�E������E��EF��AB��BC�ڵ�F������ABC=40��������DEF�Ķ�����
�뽫����Ľ����̲�������������գ����ɻ���ѧʽ��
������DE��BC�����DEF= ����������
��EF��AB���� =��ABC����������
���DEF=��ABC��������������
�ߡ�ABC=40�������DEF= ����
��2��Ӧ������ͼ����ֱ��AB��BC��AC�����ཻ������ֱ�Ϊ��A��B��C����D���߶�AB���ӳ�����������D��DE��BC��AC�ڵ�E������E��EF��AB��BC�ڵ�F������ABC=60��������DEF= ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����������У����ж�ֱ��L1��L2����( )

A. ��2=��3 B. ��l=��3 C. ��4+��5=180![]() D. ��2=��4
D. ��2=��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С�����������У���AOB�Ķ�����ڸ���ϣ�
��1��B�����y��ĶԳƵ�����Ϊ ��
��2������AOB����ƽ��3����λ���ȵõ���A1O1B1���뻭����A1O1B1��
��3���ڣ�2���������£�A1������Ϊ ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com