练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，CD是AB边上的高，则AD长为（　　）cm．
    A．$\frac{3}{5}$B．$\frac{4}{5}$C．$\frac{16}{5}$D．$\frac{9}{5}$

    分析 根据勾股定理求得AB，由三角形相似得到比例式代入数值即可求出．

    解答 解：∵∠ACB=90°，CD是AB边上的高，
    ∴∠ACB=∠ADC=90°，
    ∵AC=3cm，BC=4cm，
    ∴AB=$\sqrt{{{AC}^{2}+BC}^{2}}$=5cm，
    ∵∠A=∠A，
    ∴△ACD∽△ABC，
    ∴$\frac{AC}{AB}$=$\frac{AD}{AC}$，
    ∴AD=$\frac{{AC}^{2}}{AB}$=$\frac{9}{5}$．
    故选D．

    点评 本题考查了相似三角形的判定和性质，勾股定理，证明△ACD∽△ABC是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．解方程：3a2-32a+52=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

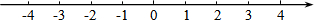    19．解不等式组，并把解集在数轴上表示出来．
    $\left\{\begin{array}{l}{x-3（x-2）≥4}\\{\frac{5x}{6}+1＞\frac{x-3}{4}}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

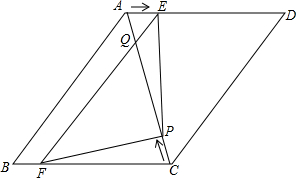    17．如图，在?ABCD中，AB=6cm，AD=AC=5cm，点P由C出发沿CA方向匀速运动，速度为1cm/s；同时，线段EF由AB出发沿AD方向匀速运动，速度为1cm/s，交AC于Q，连接PE、PF，若运动时间为t（s）（0＜t＜2.5）．解答下列问题：
    （1）当t为何值时，PE∥CD？
    （2）试判断△PEF形状，并说明理由；
    （3）请求五边形ABEFPE的面积；
    （4）求△PFC的面积s与t的函数关系式：并确定当t为何值时，s有最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

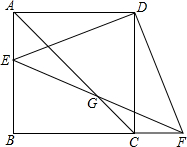    4．如图，在正方形ABCD中，AB=1，E为边AB上的一点（点E不与端点A、B重合），F为BC延长线上的一点，且AE=CF，联结EF交对角线AC于点G．
    （1）求证：DE=DF；
    （2）联结DG，求证：DG⊥EF；
    （3）设AE=x，AG=y，求y关于x的函数解析式及定义域．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，抛物线y=$\frac{1}{2}$x2+bx+c与y轴交于点C（0，-4），与x轴交于点A、B，且B点的坐标为（2，0）．
    （1）求抛物线的解析式；
    （2）若点P是AB上的一个动点，过点P作PE∥AC交BC于点E，连接CP，求△PCE面积的最大值；
    （3）在（2）的条件下，若点D为OA的中点，点M是线段AC上一点，当△OMD为等腰三角形时，连接MP、ME，把△MPE沿着PE翻折，点M的对应点为点N，求点N的坐标，并判断点N是否在抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．某初中学校现有学生500人，计划一年后男生增加5%，女生增加4%，这样总人数将增加4.5%，设该校现有男生x人，女生y人，可得方程组为（　　）
    A．$\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=4.5%}\end{array}\right.$B．$\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=500×4.5%}\end{array}\right.$
    C．$\left\{\begin{array}{l}{x+y=500}\\{105%x+104%y=500+4.5%}\end{array}\right.$D．$\left\{\begin{array}{l}{x+y=500}\\{104%x+105%y=500×104.5%}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

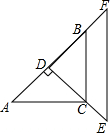    18．已知：有两块完全相同的含45°角的三角板，如图，将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处，这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

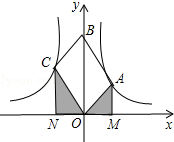    19．如图，OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线$y=\frac{k_1}{x}$和y=$\frac{{k}_{2}}{x}$的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：①$\frac{AM}{CN}$=$\frac{|{k}_{1}|}{|{k}_{2}|}$；②阴影部分面积是$\frac{1}{2}$（k1+k2）；③当∠AOC=90°时，|k1|=|k2|；④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．其中正确的结论是（　　）
    A．①②③B．②④C．①③④D．①④

    查看答案和解析>>

    同步练习册答案