
【题目】在△ABC和△A1B1C1中,下列命题中真命题的个数为( )
(1)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(2)若AC∶A1C1=CB∶C1B1,∠C=∠C1,则△ABC∽△A1B1C1;
(3)若AB=kA1B1,AC=kA1C1(k≠0),∠A=∠A1,则△ABC∽△A1B1C1;
(4)若S△ABC=![]() ,则△ABC∽△A1B1C1.
,则△ABC∽△A1B1C1.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据相似三角形的性质①有两角相等的两个三角形相似,②有两边的比相等,并且它们的夹角也相等的两个三角形相似,③有三组对应边的比相等的两三角形相似,逐个判断即可.
解:如图:
(1)![]() ∠A=∠
∠A=∠![]() ,∠C=∠
,∠C=∠![]() ,
,
![]() △ABC~△
△ABC~△![]() ,
,![]() (1)正确;
(1)正确;
(2)AC∶A1C1=CB∶C1B1,∠C=∠C1, ![]() △ABC~△
△ABC~△![]() ,(2)正确;
,(2)正确;
(3) ![]() AB=kA1B1,AC=kA1C1(k≠0),
AB=kA1B1,AC=kA1C1(k≠0),![]()
![]() =k
=k
又![]() ∠A=∠A1
∠A=∠A1![]() △ABC~△
△ABC~△![]() ,(3)正确;
,(3)正确;
(4)当AB=2,AB边上的高为1,![]() =1,
=1,![]() 边上的高为2时, S△ABC=
边上的高为2时, S△ABC=![]() 此时△ABC和△
此时△ABC和△![]() 不相似,故(4)错误;
不相似,故(4)错误;
所以正确的有(1)(2)(3),故C选项是正确的.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
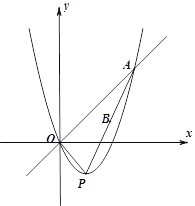
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“我爱我的祖国”教育知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其预赛成绩如图所示:
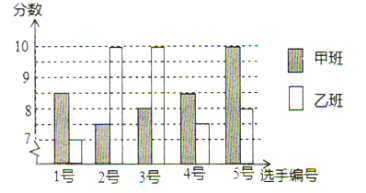
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
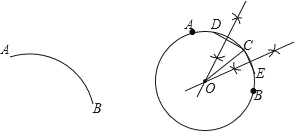
【题目】下面是“作出弧AB所在的圆”的尺规作图过程.
已知:弧AB.
求作:弧AB所在的圆.
作法:如图,
(1)在弧AB上任取三个点D,C,E;
(2)连接DC,EC;
(3)分别作DC和EC的垂直平分线,两垂直平分线的交点为点O.
(4)以 O为圆心,OC长为半径作圆,所以⊙O即为所求作的弧AB所在的圆.
请回答:该尺规作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,连接BE,CD相交于点O,连接DE,下列结论:①![]() =
=![]() ;②
;②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() ,其中正确的个数有( )
,其中正确的个数有( )
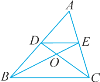
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
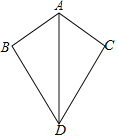
【题目】如图给出下列五个等量关系
①AB=AC;②BD=CD;③∠BAD=∠CAD;④∠B=∠C=90°;⑤∠BDA=∠CDA.
请你以其中两个为条件,另三个中的一个为结论,写出一个正确命题(只需写出一种情况),并加以证明.
解:我选作为题设的等量关系是: 、 ;
作为正确结论的等量关系是 .
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com