
【题目】如图,在△ABC中,∠ACB=900,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.
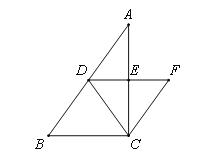
(1)求证:DE=EF;
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
【答案】(1)见解析.
(2)见解析.
【解析】
(1)通过由ASA证明△AED≌△CEF得出结论.
(2)如图,经过转换,将∠B转换成∠ADE,从而通过证明∠DGC=∠1和∠2=∠A得出结论.
证明:(1)∵在△ABC中,∠ACB=900,点D为边AB的中点,
∴DC=DA(直角三角形斜边上中线等于斜边的一半).
∵DE∥BC,∴AE=CE(平行线等分线段的性质),∠A=∠FCE(平行线的内错角相等).
又∵∠AED=∠CEF(对顶角相等),∴△AED≌△CEF(ASA).
∴DE=EF(全等三角形对应边相等).
(2)如图,∵在△ABC中,∠ACB=900,点D为边AB的中点,
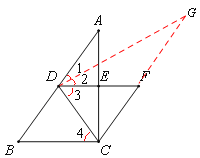
∴DC=DB(直角三角形斜边上中线等于斜边的一半).
∴∠B=∠4(等边对等角).
又∵DE∥BC,∴∠4=∠3,∠B=∠ADE.
∵DG⊥DC,∴∠2+∠3=900,即∠2+∠D=900.
∵∠ACB=900,∴∠A+∠D=900.∴∠2=∠A.
∵CF∥AB,∴∠DGC=∠1.
∴∠B=∠ADE=∠2+∠1=∠A+∠DGC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】同样大小的黑色棋子按图中所示的规律摆放:

(1)填写下表:
图形序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
图中棋子数 | 6 | 9 |
|
|
|
|
| … |
(2)照这样的方式摆下去,写出摆第n(n为正整数)个图形所需黑色棋子的颗数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
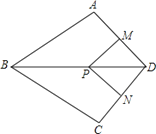
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有两定点A、B,点![]() 表示的数为6,点B在点A的左侧,且AB=20,动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒(t>0).
表示的数为6,点B在点A的左侧,且AB=20,动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒(t>0).
![]()
(1)写出数轴上点B表示的数______,点P表示的数用含t的式子表示:_______;
(2)设点M是AP的中点,点N是PB的中点.点P在直线AB上运动的过程中,线段MN的长度是否会发生变化?若发生变化,请说明理由;若不变化,求出线段MN的长度.
(3)动点R从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、R同时出发;当点P运动多少秒时?与点R的距离为2个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲三角形的周长为![]() ,乙三角形的第一条边长为
,乙三角形的第一条边长为![]() ,第二条边长为
,第二条边长为![]() ,第三条边比第二条边短
,第三条边比第二条边短![]() .
.
(1)求乙三角形第三条边的长;
(2)甲、乙两三角形的周长哪个大?试说明理由;
(3)a、b都为正整数,甲、乙两三角形的周长在数轴上表示的点分别为A、B,若A、B两点之间恰好有18个“整数点”(点表示的数为整数),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果种植大户小芳,为了吸引更多的顾客,组织了观光采摘游活动,每一位来采摘水果的顾客都有一次抽奖机会,在一只不透明的盒子里有A(苹果),B(梨子),C(葡萄),D(葡萄)四张外形完全相同的卡片,抽奖时先随机抽取一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图或列表的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com