
【题目】如图,在△ABC中,∠A=45°.以AB为直径的⊙O与BC相切于B,交AC于点D,CO的延长线交⊙O于点E,过点作弦EF⊥AB,垂足为点G.
(1)求证:①EF∥CB,②AD=CD;
(2)若AB=10,求EF的长.
【答案】
(1)证明:①连接BD.

∵BC是⊙O的切线,
∴AB⊥BC,
∵EF⊥AB,
∴EF∥AB.
②∵∠ABC=90°,∠A=45°,
∴∠A=∠ACB=45°,
∴BA=BC,
∵AB是直径,
∴∠ADB=90°,
∴BD⊥AC,
∴AD=DC
(2)解:∵AB=CB=10,
∴OE=OB=5,
在Rt△BOC中,OC= ![]() =5
=5 ![]() ,
,
∵EG∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EG=2 ![]() ,
,
∵OA⊥EF,
∴EG=GF=2 ![]() ,
,
∴EF=4 ![]() .
.
【解析】①已知BC是⊙O的切线及EF⊥AB,易证得EF∥AB;’②已知AB是圆的直径,因此连接BD,证得∠ADB=90°,再证明BA=BC,根据等腰三角形的性质即可得出结论。
(2)在Rt△BOC中利用勾股定理求出OC的长,由EG∥BC,根据平行线分线段成比例定理,得出对应线段成比例,建立方程求出EG的长,再利用垂径定理即可解决问题。
【考点精析】利用平行线的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在四边形ABCD中,AD∥BC,且BC=12cm,AD=18cm,P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,Q以4cm/s的速度由C向B运动,问当多少秒时,直线QP将四边形ABCD截出一个平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )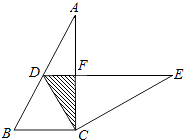
A.30,2
B.60,2
C.60, ![]()
D.60, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,正方形ABFG和FCDE的顶点均和小正方形的顶点重合.
(1)建立平面直角坐标系,使得B,C的坐标分别为(0,0),(4,0),并写出点A的坐标;
(2)直接写出正方形FCDE的边长;
(3)连接EG,直接比较三角形BCF和三角形GEF的面积大小 (用“大于”,“小于”,“等于”作答)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面![]() 倒下到
倒下到![]() 的位置,连接
的位置,连接![]() ,设
,设![]() 、
、![]() 、
、![]() ,请利用四边形
,请利用四边形![]() 的面积验证勾股定理.
的面积验证勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )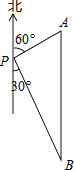
A.60海里
B.45海里
C.20 ![]() 海里
海里
D.30 ![]() 海里
海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com