
 如图,△ABO和△CDO都是等腰直角三角形,∠AOB=∠COD=90°,点D在AB上.
如图,△ABO和△CDO都是等腰直角三角形,∠AOB=∠COD=90°,点D在AB上.
|


科目:初中数学 来源: 题型:
 (2012•仁寿县模拟)如图将△ABO沿x轴的正方向平移4个单位得到△A′B′O′,再绕0′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,4),B点坐标为(-3,0);
(2012•仁寿县模拟)如图将△ABO沿x轴的正方向平移4个单位得到△A′B′O′,再绕0′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,4),B点坐标为(-3,0);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
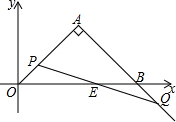 如图,△ABO中,∠A=90°,AO=AB=2
如图,△ABO中,∠A=90°,AO=AB=2 ,OB=4,以O为原点,OB所在的直线为x轴建立直角坐标系,在O和B处分别有动点P和Q,P从O沿OA向A运动,Q从B沿AB的延长线运动,两点同时出发,速度都为
,OB=4,以O为原点,OB所在的直线为x轴建立直角坐标系,在O和B处分别有动点P和Q,P从O沿OA向A运动,Q从B沿AB的延长线运动,两点同时出发,速度都为 ,运动的时间为t,且0<t<2.
,运动的时间为t,且0<t<2.查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省昆明三中、滇池中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且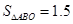 .(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程
.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程 的解;(4)使一次函数的值大于反比例函数的值的
的解;(4)使一次函数的值大于反比例函数的值的 的取值范围;
的取值范围;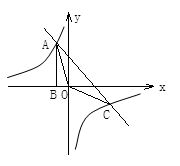
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
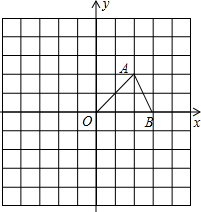 (1)如图,△ABO的两个顶点的坐标分别为A(2,2),B(3,0),将△ABC绕O点逆时针旋转90°,得到△DEO,则D点的坐标为______,点E的坐标为______.
(1)如图,△ABO的两个顶点的坐标分别为A(2,2),B(3,0),将△ABC绕O点逆时针旋转90°,得到△DEO,则D点的坐标为______,点E的坐标为______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com