
��ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������

 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��֪�����ߵĶ���Ϊ(-1,-3)����y��Ľ���Ϊ(0,-5)�������ߵĽ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ�ڵڶ�����ѧ�Ծ� ���ͣ������
�Ķ����ϣ�С����һ�������Խ�ĺ�ѧ��������ѧϰ���й�Բ���������ʺ�����δ�����ֲ��ĵ�����Բ��������ص�һ�����⣺
��ͼ1����֪PC�ǡ�O�����ߣ�AB�ǡ�O��ֱ�����ӳ�BA������PC��P������AC��BC��OC��
��ΪPC�ǡ�O�����ߣ�AB�ǡ�O��ֱ�������ԡ�OCP=��ACB=90�㣬���ԡ�1=��2��
����Ϊ��B=��1�����ԡ�B=��2��
�ڡ�PAC���PCB�У�����Ϊ����P=��P�����ԡ�PAC�ס�PCB������ ����PC2=PA•PB��
����PC2=PA•PB��
������չ��
�������PB��������O��Բ��O����ͼ2����ʽPC2=PA•PB������������֤����Ľ��ۣ�
�ۺ�Ӧ�ã�
������ͼ3����O�ǡ�ABC�����Բ��PC�ǡ�O�����ߣ�C���е㣬BA���ӳ��߽�PC�ڵ�P��
��1����AB=PA����PC=12ʱ����PA��ֵ��
��2��D��BC���е㣬PD��AC�ڵ�E����֤��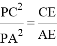 ��
��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ�ڵڶ�����ѧ�Ծ� ���ͣ������
����ABC�ס�DEF����ABC���DEF�������Ϊ4��9����AB��DE=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ�ڵڶ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�O�У� =
= ����BAC=50�㣬���AEC�Ķ���Ϊ��������
����BAC=50�㣬���AEC�Ķ���Ϊ��������

A. 65�� B. 75�� C. 50�� D. 55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���㽭ʡ�������п���ѧ�����Ծ������� ���ͣ������
���㣺�� ����2+���Щ�2017��0+sin60��+|
����2+����2017��0+sin60��+| ��2|
��2|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���㽭ʡ�������п���ѧ�����Ծ������� ���ͣ���ѡ��
��ͼ��������ϵ�з���һ����OABC����֪��ABC=60�㣬��B��y���ϣ�OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60�㣬������ת2017�Σ���B���������ΪB1��B2��B3��������B2017������Ϊ��������
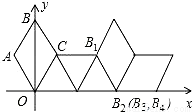
A. ��1345,0�� B. ��1345.5��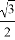 �� C. ��1345��
�� C. ��1345��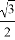 �� D. ��1345.5��0��
�� D. ��1345.5��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��������2016-2017ѧ�����꼶��ѧ�ڣ������ƣ����п�����ѧ�Ծ� ���ͣ������
��֪��AOB=40�㣬OC��OA,ODΪ��BOC��ƽ���ߣ����AODΪ________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ�ڿ�ѧ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���������ж�AB��EF�������У�������
�١�B+��BFE=180�㣻�ڡ�1=��2���ۡ�3=��4���ܡ�B=��5��
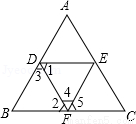
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com