
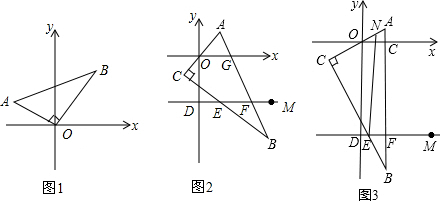
分析 (1)求出OA、OB,根据根据三角形的面积公式直接计算即可;
(2)①在如图2中,过C作CH∥x轴,则∠ACH=∠ACH=50°,求出∠ECH,由CH∥DM,可得∠ECH+∠CEF=180°,由此即可解决问题;
(3)首先证明∠NEC=∠CED,由∠NEF=2(90°-∠CED),∠CED=∠COD=90°-∠AOG,推出∠AOG=90°-CED,即可推出∠NEF=2∠AOG.
解答 解:(1)∵点A坐标为(-3,3),点B坐标为(5,5),
∴OA=3$\sqrt{2}$,OB=5$\sqrt{2}$,OA⊥OB,
∴S△ACB=$\frac{1}{2}$×$3\sqrt{2}$×5$\sqrt{2}$=15,
故答案为15.
(2)①在如图2中,过C作CH∥x轴,则∠ACH=∠ACH=50°,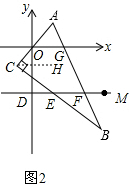
∵∠ACB=90°,∴∠ECH=40°,
∵DM∥x轴,
∴CH∥DM,
∴∠ECH+∠CEF=180°,
∴∠CEF=180°-∠ECH=140°.
②如图3中,
∵∠NEC+∠CEF=180°,∠CEF+∠CED=180°,
∴∠NEC=∠CED,
∵∠CED+∠NEC+∠NEF=180°,
∴∠NEF+2∠CED=180°,
∴∠NEF=2(90°-∠CED),
∵∠CED=∠COD=90°-∠AOG,
∴∠AOG=90°-CED,
∴∠NEF=2∠AOG.
点评 本题考查三角形综合题、直角三角形的性质、平行线的性质.三角形内角和定理等知识,解题的关键是学会添加常用辅助线,构造平行线,利用平行线的性质解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
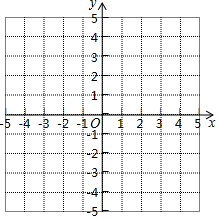 如图,在平面直角坐标系xOy中,已知A(-2,3),B(-3,1),C(-1,0),D(0,2),B1(-2,-3),请完成下列问题:
如图,在平面直角坐标系xOy中,已知A(-2,3),B(-3,1),C(-1,0),D(0,2),B1(-2,-3),请完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
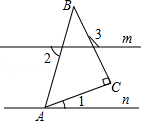 如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{16}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
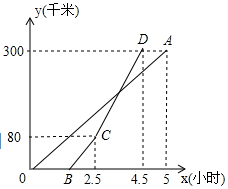 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com