
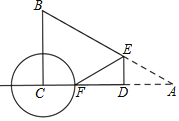
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4![]() .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
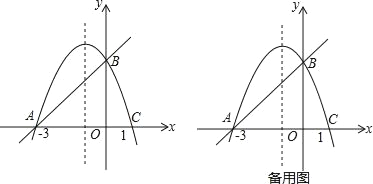
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,m),C(1,0).
(1)求m值;
(2)设点P是直线AB上方的抛物线上一动点(不与点A、B重合).
①过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求出对应的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
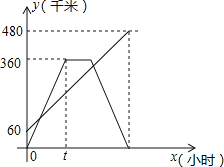
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,下列说法正确的是( )
,下列说法正确的是( )
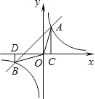
A. 点![]() 和点
和点![]() 关于原点对称 B. 当
关于原点对称 B. 当![]() 时,
时,![]()
C. ![]() D. 当
D. 当![]() 时,
时,![]() 、
、![]() 都随
都随![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m+2)x2﹣2(m+2)x﹣m+5,其中m+2>0.
(1)求该二次函数的对称轴方程;
(2)过动点C(0,n)作直线l⊥y轴.
①当直线l与抛物线只有一个公共点时,求n与m的函数关系;
②若抛物线与x轴有两个交点,将抛物线在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.当n=7时,直线l与新的图象恰好有三个公共点,求此时m的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列问题中,两个变量成反比例的是( )
A.长方形的周长确定,它的长与宽
B.长方形的长确定,它的周长与宽
C.长方形的面积确定,它的长与宽
D.长方形的长确定,它的面积与宽
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com