
【题目】如图,一渔船由西往东航行,在![]() 点测得海岛
点测得海岛![]() 位于北偏东
位于北偏东![]() 的方向,前进
的方向,前进![]() 海里到达
海里到达![]() 点,此时,测得海岛
点,此时,测得海岛![]() 位于北偏东
位于北偏东![]() 的方向,则海岛
的方向,则海岛![]() 到航线
到航线![]() 的距离
的距离![]() 等于________海里.
等于________海里.

科目:初中数学 来源: 题型:
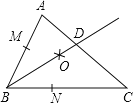
【题目】在△ABC中,∠ABC=64°,BC≠AB.小华根据下列的作法在△ABC上作图,如图所示.按要求完成下列各小题.
作法:①以点B为圆心,适当长度为半径画弧,交BA于点M,交BC于点N.
②分别以点M,N为圆心、大于![]() MN的长为半径画弧,两弧交于点O.
MN的长为半径画弧,两弧交于点O.
③连接BO并延长,交AC于点D.
(1)求∠ABD的度数.
(2)两个香料加工厂(分别是点A和点C)和一个居民区(点B)的位置示意图恰好是△ABC,两个香料加工厂想合资修建一个污水处理厂(P),好将生产所得的污水处理到合格水平再排放.为了不污染居民的生活用水,计划该污水处理厂建设在线段BD的延长线上,并且该污水处理厂与两个香料加工厂的距离相等.请你判断能否找到满足上述条件的污水处理厂的位置?并在图中利用画图说明理由.(保留作图痕迹,不要求写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
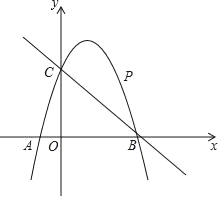
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形。
,所以这个三角形是常态三角形。
(1)若△ABC三边长分别是2,![]() 和4,则此三角形_________常态三角形(填“是”或“不是”);
和4,则此三角形_________常态三角形(填“是”或“不是”);
(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为__________________(请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2﹣EA2=AC2.

(1)求证:∠A=90°;
(2)若AB=8,BC=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com