
 已知实数a、b在数轴上的位置如图所示,化简|1-a|-$\sqrt{(a+b)^{2}}$.
已知实数a、b在数轴上的位置如图所示,化简|1-a|-$\sqrt{(a+b)^{2}}$.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
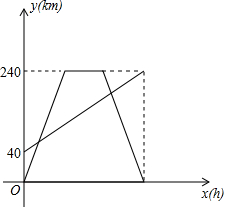 A,B两地相距240km,甲骑摩托车由A地驶往B地,出发1小时后,乙驾驶汽车由B地驶往A地,乙达到A地停留1小时后,按原路原速返回B地,恰好与甲同时到达B地,乙行驶过程中两人均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
A,B两地相距240km,甲骑摩托车由A地驶往B地,出发1小时后,乙驾驶汽车由B地驶往A地,乙达到A地停留1小时后,按原路原速返回B地,恰好与甲同时到达B地,乙行驶过程中两人均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
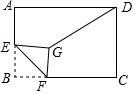 如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )
如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )| A. | $\sqrt{73}-3$ | B. | $\sqrt{34}$ | C. | 6 | D. | $\frac{32}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com