
【题目】如图,BD是□ABCD的一条对角线.AE⊥BD于点E,CF⊥BD于点F.求证:∠DAE=∠BCF.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E. 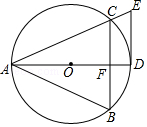
(1)求证:DE∥BC;
(2)若DF=n,∠BAC=2a,写出求CE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有500名学生.为了解全校每名学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到扇形统计图如右图:
(1)本次调查的个体是 ,样本容量是 ;
(2)扇形统计图中,乘私家车部分对应的圆心角是 度;
(3)请估计该校500名学生中,选择骑车和步行上学的一共有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=﹣ ![]() x2﹣2x+c经过点A、B,抛物线的顶点为C.
x2﹣2x+c经过点A、B,抛物线的顶点为C.
(1)∠BAO=°;
(2)求tan∠CAB的值;
(3)在抛物线上是否存在点P,能够使∠PCA=∠BAC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]()
![]() 已知点
已知点![]() ,
,![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点
已知点![]() ,
,![]() ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC. 
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①![]() ; ②假分数的倒数是真分数;③
; ②假分数的倒数是真分数;③![]() =1,所以
=1,所以![]() 、
、![]() 、
、![]() 互为倒数;④1
互为倒数;④1![]() 的倒数是
的倒数是![]() ;⑤a的倒数是
;⑤a的倒数是![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com