
 (2)S=-
(2)S=- x+6,0<x<4
x+6,0<x<4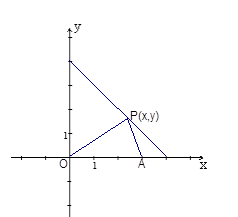
 OA·y…………………………………………………………………5分
OA·y…………………………………………………………………5分 ×3·y=
×3·y= y
y (-x+4)=-
(-x+4)=- x+6,
x+6, x+6,……………………………………………………………7分
x+6,……………………………………………………………7分




科目:初中数学 来源:不详 题型:解答题


 始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由.
始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车装载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点
,点 在
在 正半轴上,且
正半轴上,且 .动点
.动点 在线段
在线段 上从点
上从点 向点
向点 以每秒
以每秒 个单位的速度运动,设运动时间为秒.点M、N在
个单位的速度运动,设运动时间为秒.点M、N在 轴上,且
轴上,且 是等边三角形.
是等边三角形. 的边长(用的代数式表示),并求出当等边
的边长(用的代数式表示),并求出当等边 的顶点
的顶点 运动到与原点
运动到与原点 重合时的值;
重合时的值; 的中点
的中点 ,以
,以 为边在
为边在 内部作如图2所示的矩形
内部作如图2所示的矩形 ,点
,点 在线段
在线段 上.设等边
上.设等边 和矩形
和矩形 重叠部分的面积为
重叠部分的面积为 ,请求出当
,请求出当 秒时,
秒时, 与的函数关系式,并求出
与的函数关系式,并求出 的最大值.
的最大值.



查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com