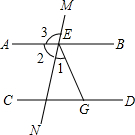练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，AB∥CD，∠1：∠2：∠3=1：4：5
    （1）求∠3的度数；
    （2）射线EB是∠MEG的平分线吗？为什么？

    分析 （1）由∠1：∠2：∠3=1：4：5，设∠1=x，∠2=4x，∠3=5x，由∠2+∠3=180°，得到4x+5x=180°，解得：x=20°，所以∠3=5×20°=100°．
    （2）射线EB是∠MEG的平分线，利用平角分别求出∠MEB=180°-∠3=180°-100°=80°，∠BEG=180°-∠1-∠2=180°-20°-80°=80°，得到∠BEG=∠MEB，射线EB是∠MEG的平分线．

    解答 解：（1）由∠1：∠2：∠3=1：4：5，设∠1=x，∠2=4x，∠3=5x，
    ∵∠2+∠3=180°，
    ∴4x+5x=180°，
    解得：x=20°，
    ∴∠3=5×20°=100°．
    ∠1=20°，∠2=80°．
    （2）射线EB是∠MEG的平分线，
    ∵∠3=100°，
    ∴∠MEB=180°-∠3=180°-100°=80°，
    ∵∠1+∠2+∠BEG=180°，
    ∴∠BEG=180°-∠1-∠2=180°-20°-80°=80°，
    ∴∠BEG=∠MEB，
    ∴射线EB是∠MEG的平分线．

    点评 本题考查了角的计算，解决本题的关键是由∠1：∠2：∠3=1：4：5，设∠1=x，∠2=4x，∠3=5x，利用平角分别求出∠1，∠2，∠3的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．下个各式成立的是（　　）
    A．$\sqrt{（-2）^{2}}$=-2B．$\sqrt{（-5）^{2}}$=-5C．$\sqrt{（-6）^{2}}$=6D．$\sqrt{{x}^{2}}$=x

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在△ABC中，∠B=∠C，点D、E分别在BC、AC上，AD=AE，试猜想∠BAD和∠EDC有何数量关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$（a＞b＞0），则m的取值范围是1＜m＜2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

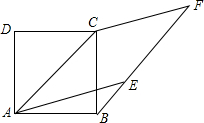    9．如图，正方形ABCD中，AB=$\sqrt{2}$，点F为正方形ABCD外一点，点E在BF上，且四边形AEFC是菱形．
    （1）求菱形AEFC的面积；
    （2）求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知关于x，y的方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-2y=m}\end{array}\right.$．求这个方程组的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

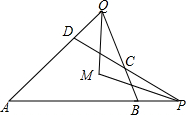    6．如图，已知，四边形ABCD，P，Q在AB、AD的延长线上，PM，QM分别平分∠APC和∠AQC．
    （1）若∠ADC=∠ABC=90°，求证：PM⊥QM；
    （2）若∠A+∠DCB=180°，则PM⊥QM还成立啊？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

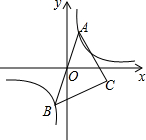    3．如图，已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=$\frac{k}{x}$（k＜0）上运动，则k的值是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：$\sqrt{12}$+（π-2014）0+（$\frac{1}{2}$）-1-4sin60°．

    查看答案和解析>>

    同步练习册答案