
【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.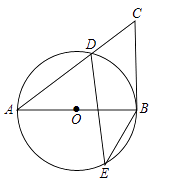
(1)求证:BC为⊙O的切线.
(2)若sinA= ![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
【答案】
(1)证明:∵∠A与∠E所对的弧是 弧BD![]() ,
,
∴∠A=∠E,
又∵∠E+∠C=90°,
∴∠A+∠C=90°,
∴∠ABC=180°﹣90°=90°,
∵AB为直径,
∴BC为⊙O的切线.
(2)解:∵sinA= ![]() ,BC=6,
,BC=6,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴AC=10,
在Rt△ABC中,
∴AB= ![]() =
= ![]() =8,
=8,
又∵AB为直径,
∴⊙O的半径是 ![]() ×8=4.
×8=4.
【解析】(1)根据同弧所对的圆周角相等得∠A=∠E,同等量代换得∠A+∠C=90°,再由三角形内角和得∠ABC=90°,根据切线的判定即可得BC为⊙O的切线.
(2)由三角函数正弦定义得:sinA=![]() =
=![]() ,从而得AC=10,在Rt△ABC中,根据勾股定理得AB=8,从而得⊙O的半径.
,从而得AC=10,在Rt△ABC中,根据勾股定理得AB=8,从而得⊙O的半径.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上.将直角三角板
上.将直角三角板![]() 在平面内绕点
在平面内绕点![]() 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线![]() 与直线
与直线![]() 的夹角为60°,则
的夹角为60°,则![]() 的度数为___.
的度数为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,![]() 与
与![]() 、
、![]() 、
、![]() 的数量关系为____.
的数量关系为____.
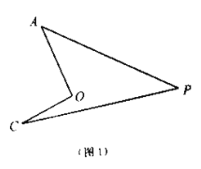
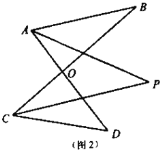
(2)如图(2),已知![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
由(1)结论得:![]()
所以![]() 即
即![]()
因为![]()
![]()
所以![]()
所以![]() .
.
解决问题:
(1)如图(3),直线![]() 平分
平分![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系是______;
的数量关系是______;
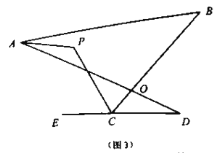
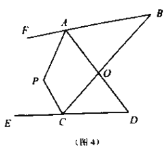
(2)如图(4),直线![]() 平分
平分![]() 的外角
的外角![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
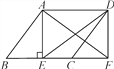
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() 可化为3x=6.
可化为3x=6.
D.方程 ![]() 系数化为1,得x=﹣1
系数化为1,得x=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.![]()
B.3
C.3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com