练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框（如图），已知该三角形的底边上的高AD=40cm，请问AB、AC、BC的长分别是多少？

    分析 设出腰的长，则底边的长可表示出来，又已知等腰三角形的高，在Rt△ABD中运用勾股定理可解得腰长．

    解答 解：设腰长AB=AC=xcm，则BC=160-2x，BD=$\frac{1}{2}$BC=80-x，
    在Rt△ABD中，AB2=BD2+AD2，
    即x2=（80-x）2+402，
    解之得：x=50，
    ∴AB=AC=50cm，BC=160-2×50=60cm．

    点评 本题考查了等腰三角形的性质，解答本题的关键是掌握等腰三角形三线合一的性质以及勾股定理的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．指出下列平面图形各是什么几何体的展开图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

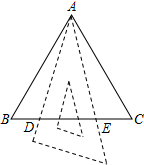    2．如图，△ABC是边长为a的等边三角形，将三角板的30°角的顶点与A重合，三角板30°角的两边与BC交于D、E两点，则DE长度的取值范围是（2$\sqrt{3}$-3）a≤DE≤$\frac{1}{2}$a．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

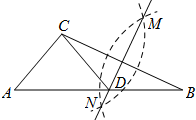    19．如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD．若CD=AC，∠B=25°，则∠ACB的度数为105°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6． 一个等腰三角形工件，尺寸标注如图，则△ABC的面积为512$\sqrt{21}$mm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．规定一种运算“*”，a*b=$\frac{1}{3}$a-$\frac{1}{4}$b，则方程x*2=1*x的解为$\frac{10}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为E，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．π精确到个位是3，精确到十分位是3.1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，在△ABC中，AB=AC，AD是高，能直接判断△ABD≌△ACD的依据是（　　）
    A．SSSB．SASC．HLD．ASA

    查看答案和解析>>

    同步练习册答案