
分析 本题目转化为在x轴上求一点到定点A(0,1),定点B(3,3)的距离和的最小值即可.
解答 解:∵y=-x+3,
∴$\sqrt{{x}^{2}+1}$+$\sqrt{{y}^{2}+9}$=$\sqrt{{x}^{2}+1}$+$\sqrt{(3-x)^{2}+9}$
∴求$\sqrt{{x}^{2}+1}$+$\sqrt{(3-x)^{2}+9}$的最小值,可以看成在x轴上找一点P(x,0),使得点P到点A(0,1),点B(3,3)的距离之和最小,
如图,作BM⊥OA于M,A,A$′\\;\$关于原点对称,连接BA′与x轴的交点就是所求的点P.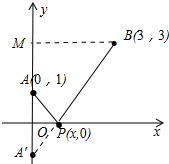
在Rt△A′BM中,∵∠BMA′=90°,BM=3,A′M=4,
∴BA′=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴PA+PB的最小值=BA′=5,
故答案为5
点评 本题看成轴对称-最小值问题、两点间距离公式等知识,解题的关键是把问题转化为在x轴上求一点到定点A(0,1),定点B(3,3)的距离和的最小值问题,是数形结合的好题目,属于中考常考题型.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | ② | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:3:5 | B. | 2:3:4 | C. | 4:3:2 | D. | 5:3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-100\frac{1}{3}<-101$ | B. | -100<-101 | C. | $-100>-100\frac{1}{3}$ | D. | $-100\frac{1}{3}>-100$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
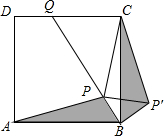 如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度)
如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com