
【题目】如图,已知直角梯形![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点,过
边上的一动点,过![]() 作线段
作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,并交射线
,并交射线![]() 于点
于点![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长;
的长;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)如图2,联结![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.



【答案】(1)BC=5;(2)![]() ;(3)
;(3)![]() 的长为
的长为![]() 或3或
或3或![]() .
.
【解析】
(1)根据垂直平分线性质可知![]() ,设
,设![]() ,
,![]() ,在
,在![]() 中用勾股定理求出
中用勾股定理求出![]() ,即可解答;
,即可解答;
(2)联结![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,消去二次项即可得到
,消去二次项即可得到![]() 与
与![]() 的函数关系式;根据点
的函数关系式;根据点![]() 是
是![]() 边上的一动点结合(1)即可得出
边上的一动点结合(1)即可得出![]() 的定义域;
的定义域;
(3)分三种情况讨论,分别画出图形,根据相等的边用勾股定理列方程求解即可.
解:(1)∵梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)联结![]() ,
,![]() ,
,
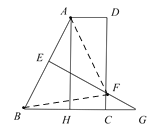
∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
(3)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]()
当![]() 是等腰三角形时
是等腰三角形时
①∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
②![]()
取![]() 中点
中点![]() ,联结
,联结![]()
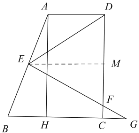
∵![]() 为
为![]() 的中点
的中点
∴![]() 为梯形中位线
为梯形中位线
∴![]()
∵![]()
∴![]() 为
为![]() 中点,
中点,
∴此时![]() 与
与![]() 重合
重合
∴![]()
③![]()
联结![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]()
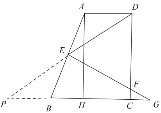
此时![]() .
.
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴在![]() 中,
中,![]() ,
,
∵![]()
∴解得![]() ,
,![]() (不合题意含去)
(不合题意含去)
∴综上所述,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长为
的长为![]() 或3或
或3或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=25°,∠ADC=115°,O为AB的中点,以点O为圆心、AO长为半径作圆,恰好点D在⊙O上,连接OD,若∠EAD=25°,下列说法中不正确的是( ) 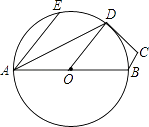
A.D是劣弧 ![]() 的中点
的中点
B.CD是⊙O的切线
C.AE∥OD
D.∠DOB=∠EAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,M![]() 表示a,b,c这三个数的平均数,min
表示a,b,c这三个数的平均数,min![]() 表示a,b,c这三个数中最小的数,如:
表示a,b,c这三个数中最小的数,如:
M![]() ,min
,min![]() =-1;
=-1;
M![]() ,min
,min![]() =
=![]() ;
;
解决下列问题:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min![]() =2,则x的取值范围是______________;
=2,则x的取值范围是______________;
(3) ①若M![]() =min
=min![]() ,那么x=______________;
,那么x=______________;
②根据①,你发现结论“若M![]() =min
=min![]() ,则______________;(填a,b,c的大小关系);
,则______________;(填a,b,c的大小关系);
③运用②解决问题:(写出求解的过程)
若M![]() =min
=min![]() ,
,
求x+y 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成,若完成该工程甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
B.
C.
D.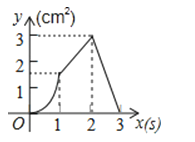
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com