
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不发生变化.
【解析】试题分析:(1)由等边三角形的性质得出∠BAC=∠DAE,容易得出结论;
(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论;
解:(1)∠BAD=∠CAE;理由:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAD=∠CAE;
(2)∠DCE=60°,不发生变化;理由如下:
∵△ABC是等边三角形,△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE.
∴∠ABD=120°,∠BAC﹣∠BAE=∠DAE﹣∠BAE
∴∠DAB=∠CAE.
在△ABD和△ACE中,
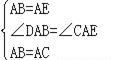 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD=120°.
∴∠DCE=∠ACE﹣∠ACB=120°﹣60°=60°.
点睛:本题考查了全等三角形的判定与性质以及等边三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在学了三角形的角平分线后,遇到下列4个问题,请你帮他解决.如图,在△ABC中,∠BAC= 50°,点I是∠ABC、∠ACB平分线的交点.

问题(1):填空:∠BIC=_________°.
问题(2):若点D是两条外角平分线的交点,则∠BDC=_________°.
问题(3):若点E是内角∠ABC、外角∠ACG的平分线的交点,则∠BEC与∠BAC的数量关系是________;
问题(4):在问题(3)的条件下,当∠ACB等于__________°时,CE∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,点
,点![]() 点
点![]() 分别在射线
分别在射线![]() ,射线
,射线![]() 上,若点
上,若点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 点
点![]() 关于
关于![]() 对称,
对称, ![]() 与
与![]() 相交于点
相交于点![]() ,有以下命题:①
,有以下命题:①![]() ;②
;②![]() ;③若
;③若![]() ,
, ![]() ;④
;④![]() 是等腰直角三角形,则正确的命题有( ).
是等腰直角三角形,则正确的命题有( ).

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
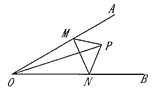
【题目】如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB =30![]() ,则△PMN周长的最小值为________.
,则△PMN周长的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若![]() , 求m和n的值
, 求m和n的值
解:∵![]()
∴![]()
∴![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
问题:(1)若![]() ,求
,求![]() 的值.
的值.
(2)已知a,b,c是△ABC的三边长,满足![]() ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.
问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.

请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;补全条形统计图;
(2)求出C类人数占总调查人数的百分比及扇形统计图中![]() 类所对应扇形圆心角的度数.
类所对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com