
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
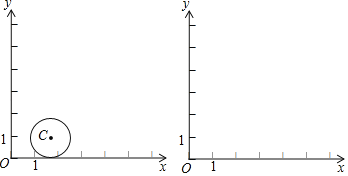
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
【答案】(1)①﹣3;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①把Q(1,a)代入y=x-4,可求出a值,根据理想值定义即可得答案;②由理想值越大,点与原点连线与![]() 轴夹角越大,可得直线
轴夹角越大,可得直线![]() 与
与![]() 相切时理想值最大,
相切时理想值最大,![]() 与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论
与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论![]() 与
与![]() 轴及直线
轴及直线![]() 相切时,LQ 取最小值和最大值,求出
相切时,LQ 取最小值和最大值,求出![]() 点横坐标即可;(3)根据题意将点
点横坐标即可;(3)根据题意将点![]() 转化为直线
转化为直线![]() ,
,![]() 点理想值最大时点
点理想值最大时点![]() 在
在![]() 上,分析图形即可.
上,分析图形即可.
(1)①∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴点![]() 的“理想值”
的“理想值”![]() =-3,
=-3,
故答案为:﹣3.
②当点![]() 在
在![]() 与
与![]() 轴切点时,点
轴切点时,点![]() 的“理想值”最小为0.
的“理想值”最小为0.
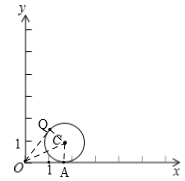
当点![]() 纵坐标与横坐标比值最大时,
纵坐标与横坐标比值最大时,![]() 的“理想值”最大,此时直线
的“理想值”最大,此时直线![]() 与
与![]() 切于点
切于点![]() ,
,
设点Q(x,y),![]() 与x轴切于A,与OQ切于Q,
与x轴切于A,与OQ切于Q,
∵C(![]() ,1),
,1),
∴tan∠COA=![]() =
=![]() ,
,
∴∠COA=30°,
∵OQ、OA是![]() 的切线,
的切线,
∴∠QOA=2∠COA=60°,
∴![]() =tan∠QOA=tan60°=
=tan∠QOA=tan60°=![]() ,
,
∴点![]() 的“理想值”为
的“理想值”为![]() ,
,
故答案为:![]() .
.
(2)设直线与![]() 轴、
轴、![]() 轴的交点分别为点
轴的交点分别为点![]() ,点
,点![]() ,
,
当x=0时,y=3,
当y=0时,![]() x+3=0,解得:x=
x+3=0,解得:x=![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴tan∠OAB=![]() ,
,
∴![]() .
.
∵![]() ,
,
∴①如图,作直线![]() .
.
当![]() 与
与![]() 轴相切时,LQ=0,相应的圆心
轴相切时,LQ=0,相应的圆心![]() 满足题意,其横坐标取到最大值.
满足题意,其横坐标取到最大值.
作![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
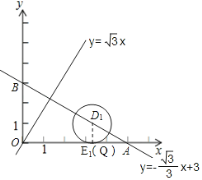
②如图
当![]() 与直线
与直线![]() 相切时,LQ=
相切时,LQ=![]() ,相应的圆心
,相应的圆心![]() 满足题意,其横坐标取到最小值.
满足题意,其横坐标取到最小值.
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
∵直线![]() 中,k=
中,k=![]() ,
,
∴![]() ,
,
∴![]() ,点F与Q重合,
,点F与Q重合,
则![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.

由①②可得,![]() 的取值范围是
的取值范围是![]() .
.
(3)∵M(2,m),
∴M点在直线x=2上,
∵![]() ,
,
∴LQ取最大值时,![]() =
=![]() ,
,
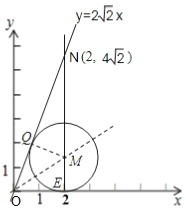
∴作直线y=![]() x,与x=2交于点N,
x,与x=2交于点N,
当![]() M与ON和x轴同时相切时,半径r最大,
M与ON和x轴同时相切时,半径r最大,
根据题意作图如下:![]() M与ON相切于Q,与x轴相切于E,
M与ON相切于Q,与x轴相切于E,
把x=2代入y=![]() x得:y=4
x得:y=4![]() ,
,
∴NE=4![]() ,OE=2,ON=
,OE=2,ON=![]() =6,
=6,
∴∠MQN=∠NEO=90°,
又∵∠ONE=∠MNQ,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:r=![]() .
.
∴最大半径为![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】一个盒子中有1个白球和2个红球,这些球除颜色外都相同.
⑴如果从盒子中随机摸出1个球,摸出红色球的概率为_____________;
⑵若从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,请通过列表或画树状图的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
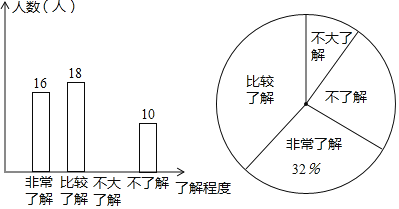
【题目】某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
(1)本次调查共抽取了多少名学生;
(2)通过计算补全条形图;
(3)若该学校共有![]() 名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
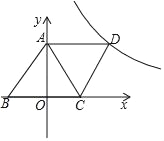
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=![]() (k为常数,k≠0,x>0)的图象经过点D.
(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=_____.
(2)已知在y=![]() 的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(﹣2,﹣2),B(0,3),C(3,3),D(4,﹣2),y是关于x的二次函数,抛物线y1经过点A、B、C,抛物线y2经过点B、C、D,抛物线y3经过点A、B、D,抛物线y4经过点A、C、D.下列判断:
①四条抛物线的开口方向均向下;
②当x<0时,至少有一条抛物线表达式中的y均随x的增大而减小;
③抛物线y1的顶点在抛物线y2顶点的上方;
④抛物线y4与y轴的交点在点B的上方.
所有正确结论的序号为_____.
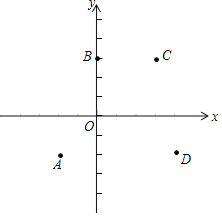
查看答案和解析>>
科目:初中数学 来源: 题型:
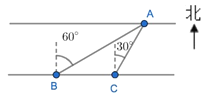
【题目】如图,在河对岸有一棵大树 A,在河岸 B 点测得 A 在北偏东 60°方向上,向东前进 200m 到达 C 点,测得 A 在北偏东 30°方向上,求河的宽度(精确到 0.1m).参考数据 ![]() ≈1.414,
≈1.414,![]() ≈1.732.
≈1.732.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)的图象经过点A(1,2).
(1)当b=1,c=﹣4时,求该二次函数的表达式;
(2)已知点M(t﹣1,5),N(t+1,5)在该二次函数的图象上,请直接写出t的取值范围;
(3)当a=1时,若该二次函数的图象与直线y=3x﹣1交于点P,Q,将此抛物线在直线PQ下方的部分图象记为C,
①试判断此抛物线的顶点是否一定在图象C上?若是,请证明;若不是,请举反例;
②已知点P关于抛物线对称轴的对称点为P′,若P′在图象C上,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
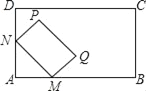
A. 4 B. 2![]() C. 7 D. 8
C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥x轴交AC于点D,求PD的最大值;
(3)将△BOC沿直线BC平移,点B平移后的对应点为点B′,点O平移后的对应点为点O′,点C平移后的对应点为点C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,求出所有符合条件的点S的坐标.
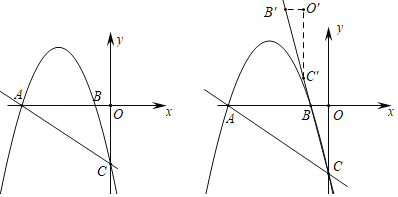
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com