
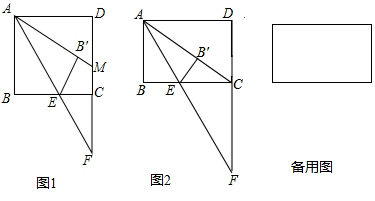
分析 (1)结论:△AMF是等腰三角形.只要证明∠MAF=∠F即可.
(2)利用(1)中结论CF=AC,用勾股定理求出AC即可,由$\frac{BE}{EC}$=$\frac{BE′}{EC}$=sin∠ACB=$\frac{AB}{AC}$=$\frac{6}{10}$=$\frac{3}{5}$,即可解决问题.
(3)分两种情形讨论①如图3中,当0<x≤6时,△ABE翻折后都在矩形内部,所以重合部分面积就是三角形面积.②如图4中,当6<x≤8时,设EB交AD于M,分别求解即可.
解答 解:(1)结论:△AMF是等腰三角形.理由如下:
如图1中,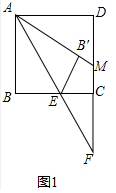
∵四边形ABCD是正方形,
∴AB∥DF,
∴∠BAE=∠F,
由翻折可知∠BAE=∠MAE,
∴∠F=∠MAE,
∴MA=MF,
∴△AMF是等腰三角形.
(2)如图2中,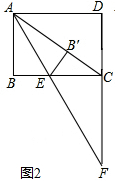
由(1)可知△ACF是等腰三角形,AC=CF,
在Rt△ABC中,∵AB=6,BC=8,
∴AC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴CF=AC=10,
∵BE=BE′,
∴$\frac{BE}{EC}$=$\frac{BE′}{EC}$=sin∠ACB=$\frac{AB}{AC}$=$\frac{6}{10}$=$\frac{3}{5}$,
故答案为10,$\frac{3}{5}$.
(3)①如图3中,当0<x≤6时,△ABE翻折后都在矩形内部,所以重合部分面积就是三角形面积,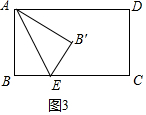
∴y=$\frac{1}{2}$•6•x=3x,
∴y=3x.
②如图4中,当6<x≤8时,设EB交AD于M,
∴重叠部分的面积=△ABE的面积减去△AB′M的面积,
设B′M=a,则EM=x-a,AM=x-a,
在Rt△AB′M中,由勾股定理可得62+a2=(x-a)2,
∴a=$\frac{{x}^{2}-36}{2x}$,
∴y=3x-$\frac{1}{2}$×6×$\frac{{x}^{2}-36}{2x}$=$\frac{3}{2}$x+$\frac{54}{x}$.
综上所述,y=$\left\{\begin{array}{l}{3x}&{(0<x≤6)}\\{\frac{3}{2}x+\frac{54}{x}}&{(6<x≤8)}\end{array}\right.$.
点评 本题考查相似三角形综合题、翻折变换、矩形的性质、正方形的性质、锐角三角函数、勾股定理、等腰三角形的判定和性质等知识,解题的关键是熟练应用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
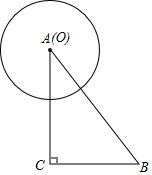 如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.
如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)-2=$-\frac{1}{4}$ | B. | $\sqrt{4}$=±2 | C. | (π-3.14)0=0 | D. | |-2|=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
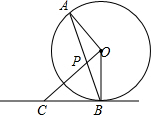 如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.
如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
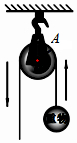 一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).
一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com