
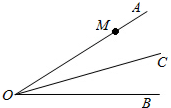
 如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是
如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是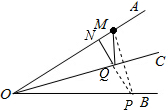 解:作M关于OC的对称点P,过P作PN⊥OA于N,交OC于Q,则此时QM+QN的值最小,
解:作M关于OC的对称点P,过P作PN⊥OA于N,交OC于Q,则此时QM+QN的值最小,| 1 |
| 2 |
| 1 |
| 2 |


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
 如图,AB∥DE,BC∥EF,那么你能判断∠ABC与∠DEF的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗?与同伴交流.
如图,AB∥DE,BC∥EF,那么你能判断∠ABC与∠DEF的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗?与同伴交流.查看答案和解析>>
科目:初中数学 来源: 题型:
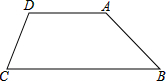 如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为
如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
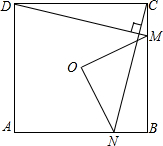 如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证:
如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com