
 如图,残阳西下时,一牧童在A处,他要把牛赶到河边BC饮水后,再赶回到D处家里.已知BC=600米,AB=500米,CD=300米.若牧童在河边BC上的点E让牛饮水,可使回家所行距离最短,求出最短距离.
如图,残阳西下时,一牧童在A处,他要把牛赶到河边BC饮水后,再赶回到D处家里.已知BC=600米,AB=500米,CD=300米.若牧童在河边BC上的点E让牛饮水,可使回家所行距离最短,求出最短距离. 分析 作D关于BC的对称点D′,连接AD′交BC于E,则AD′的长度=最短距离,求得AF=600m,FD′=AB+CD═BD+AC=800m,然后根据勾股定理求出AD′的长.
解答 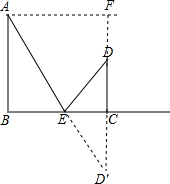 解:作D关于BC的对称点D′,连接AD′交BC于E,
解:作D关于BC的对称点D′,连接AD′交BC于E,
则AD′的长度=最短距离,
作AF⊥CD交CD的延长线于点F,如图所示,
由题意得AF=BC=600米,FD′=AB+CD═BD+AC=800m,
由勾股定理得:AD′=$\sqrt{A{F}^{2}+FD{′}^{2}}$=1000米,
∴最短距离是1000米.
点评 本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”,可以利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AB∥CD,对角线相交于点O,过O作AB的平行线交两腰于点M,N.求证:$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{2}{MN}$.
如图,梯形ABCD中,AB∥CD,对角线相交于点O,过O作AB的平行线交两腰于点M,N.求证:$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{2}{MN}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com