
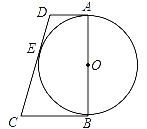
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
【答案】(1)答案见解析;(2)4.
【解析】试题分析:(1)证明△OBC≌△OEC,得出∠OBC=∠OEC=90°,证出BC为⊙O的切线;
(2)过点D作DF⊥BC于F,求出DF=AB=4,BF=AD=1,设CE=x,Rt△CDF中,根据勾股定理得出x的值即可.
试题解析:(1)连接OE,OC;如图所示:∵DE与⊙O相切于点E,∴∠OEC=90°,在△OBC和△OEC中,∵OB=OE,CB=CE,OC=OC,∴△OBC≌△OEC(SSS),∴∠OBC=∠OEC=90°,∴BC为⊙O的切线;
(2)过点D作DF⊥BC于F;如图所示:设CE=x,∵CE,CB为⊙O切线,∴CB=CE=x,∵DE,DA为⊙O切线,∴DE=DA=1,∴DC=x+1,∵∠DAB=∠ABC=∠DFB=90°,∴四边形ADFB为矩形,∴DF="AB=4" BF=AD=1,∴FC=x﹣1,Rt△CDF中,根据勾股定理得:![]() ,解得:x=4,∴CE=4.
,解得:x=4,∴CE=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣4,0)、B(0,﹣4)、C(2,0)三点,若点M为第三象限内抛物线上一动点,△AMB的面积为S,则S的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() =2
=2![]() ,
,![]() 为
为![]() 的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究

(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C=______;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案______.
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先完成下列表格:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知![]() =1.732则
=1.732则![]() =______
=______![]() =______
=______
②已知![]() =0.056,则
=0.056,则![]() =______
=______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com