
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.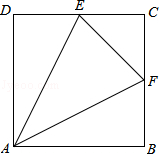
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
解:(1)证明:∵四边形ABCD为正方形,∴AB=AD,∠=90°,DC=CB,
∵E、F为DC、BC中点,∴DE= DC,BF=
DC,BF= BC。∴DE=BF。
BC。∴DE=BF。
∵在△ADE和△ABF中, ,∴△ADE≌△ABF(SAS)。
,∴△ADE≌△ABF(SAS)。
(2)由题知△ABF、△ADE、△CEF均为直角三角形,
且AB=AD=4,DE=BF= ×4=2,CE=CF=
×4=2,CE=CF= ×4=2,
×4=2,
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF
=4×4﹣ ×4×2﹣
×4×2﹣ ×4×2﹣
×4×2﹣ ×2×2=6。
×2×2=6。
解析试题分析:(1)由四边形ABCD为正方形,得到AB=AD,∠B=∠D=90°,DC=CB,由E、F分别为DC、BC中点,得出DE=BF,进而证明出两三角形全等;
(2)首先求出DE和CE的长度,再根据S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF得出结果。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:浙教版(2014) 八年级下 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源:北师大版(新课标) 九年级(下) 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.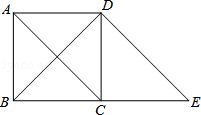
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com