8
分析:首先根据一位老师改动了方程的二次项系数后,得到的新方程有两个根为12和4,求作一个符合条件的一元二次方程,即x
2-16x+48=0,进而表示原方程是ax
2-16kx+48k=0;再根据另一位老师改动原来方程的某一个系数的符号,所得到的新方程的两个根为-2和6,求作一个符合条件的一元二次方程,即x
2-4x-12=0,此方程两边同乘以4k,得4kx
2-16kx-48k=0,从而得到a=4k,最后即可求解.
解答:利用新方程有两个根为12和4构造1个一元二次方程为:x
2-(12+4)x+12×4=0 即x
2-16x+48=0,与ax
2+bx+c=0对应.于是得到:b=-16k,c=48k.(其中k是不为0的整数.)
从而原方程为:ax
2-16kx+48k=0.同样再由另一个新方程的两个根-2和6,构造一个方程:
x
2-(-2+6)x+(-2)×6=0,
即x
2-4x-12=0.
此方程两边同乘以4k,得 4kx
2-16kx-48k=0,
它与ax
2-16kx+48k=0对应,得 a=4k,从而原方程就是:4kx
2-16kx+48k=0,所以
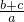
=

=8.
故答案为8.
点评:此题考查了一元二次方程根与系数的关系,能够根据已知的两根求作一个一元二次方程.

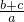 =________.
=________.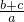 =
= =8.
=8.
